■指数方程式の解き方
両辺の底をそろえて指数同士を比較しする。
(例1)
2x = 8
2x = 23←底を2にそろえ、指数同士で比較する
x = 3
(例2)※解は実数解のみとする
4x – 3 × 2(x+1) – 16 = 0
4x – 3 × 21 × 2x – 16 = 0 ←2(x+1)をそれぞれ2x、21にわけて-3をかける
4x – 6 × 2x – 16 = 0
(2x)2 – 6 × 2x – 16 = 0 ←底を2に揃える
t = 2xとする
t2 – 6t – 16 = 0
(t + 2)(t – 8) = 0
t = -2, 8
解は実数解のみ(t > 0)であるため、t = 8
2x = 8
x = 3
なお、指数方程式について、Pythonでは、sympyを使用して解くことができる。
import sympy
# 文字列をセット
x = sympy.Symbol('x')
# xの回を求める
sympy.solve(第1引数に指数方程式(※左辺)をセット, x)※sympy.solve()を使用する場合、第1引数に設定する方程式は、右辺が「=0」のときの左辺をセットする。
■例題
以下の4問をPythonのsympyを使用して解く。
なお、解は実数解のみとする。
問題1
2x = 8
問題2
9x = 3 × 27x
問題3
4x – 3 × 2(x+1) – 16 = 0
問題4
9x – 2 × 3x+1 – 27 = 0
■サンプルコード
問題1および2について、以下の通り右辺を「=0」の状態に変換して解く
問題1
2x– 8 = 0
問題2
9x – ( 3 × 27x ) = 0
# -*- Coding:UTF-8 -*-
import sympy
# 文字列をセット
x = sympy.Symbol('x')
# 問題1
ques1 = sympy.solve(2**x - 8, x)
print('問題1:' + str(ques1))
# 問題2
ques2 = sympy.solve(9**x - 3 * 27**x, x)
print('問題2:' + str(ques2))
# 問題3
ques3 = sympy.solve(4**x - 3 * 2**(x + 1) - 16, x)
print('問題3:' + str(ques3))
# 問題4
ques4 = sympy.solve(9**x - 2 * 3**(x+1) -27, x)
print('問題4:' + str(ques4))
■実行結果
問題1:[3]
問題2:[-1]
問題3:[3, 1 + I*pi/log(2)]
問題4:[2, 1 + I*pi/log(3)]★問題3および問題4の実行結果について、「1 + I*pi/log(2)」および「1 + I*pi/log(3)」は虚数解となるため、実数解はそれぞれ「3」および「2」のみである。
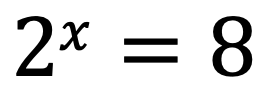
コメント