■三角関数の加法定理
すぐにわかる三角比の値、θ = 30°、45°、60°を使用して、
15°や105°の値を求めることが可能となる。
★今回はtan編のみ紹介
■三角関数の加法定理 tanの公式
tanの加法定理は以下の通り。
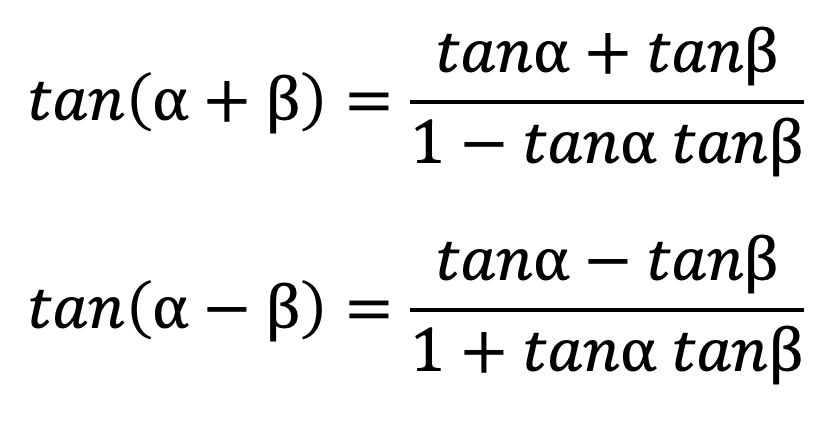
■例題
問題1
tan(165°)を加法定理を使用して求める。
問題2
tan(15°)を加法定理を使用して求める。
【特記事項】
ちなみに、pythonでは、
加法定理を使用しなくても、そのままtan(15°)、tan(75°)を求めることはできる。
■サンプルコード
▼問題1
# -*- Coding:UTF-8 -*-
import math
# 度数を変数に格納
degree = 165
tmp_degree1 = 120
tmp_degree2 = 45
# 度数をラジアンに変換
radian = math.radians(degree)
tmp_radian1 = math.radians(tmp_degree1)
tmp_radian2 = math.radians(tmp_degree2)
# 加法定理 tan(α+β)
result = math.tan(radian)
# 答え(少数第2位で表示)
print('tan(165°) = ', round(result, 2))
# 加法定理 (tanα + tanβ) / (1 - tanαtanβ)
result = (math.tan(tmp_radian1) + math.tan(tmp_radian2)) / (1 - math.tan(tmp_radian1) * math.tan(tmp_radian2))
# 答え(少数第2位で表示)
print('(tan120° + tan45°) / (1 - tan120°tan45°) = ', round(result, 2))
▼問題2
# -*- Coding:UTF-8 -*-
import math
# 度数を変数に格納
degree = 15
tmp_degree1 = 60
tmp_degree2 = 45
# 度数をラジアンに変換
radian = math.radians(degree)
tmp_radian1 = math.radians(tmp_degree1)
tmp_radian2 = math.radians(tmp_degree2)
# 加法定理 tan(α-β)
result = math.tan(radian)
# 答え(少数第2位で表示)
print('tan(15°) = ', round(result, 2))
# 加法定理 (tanα - tanβ) / (1 + tanαtanβ)
result = (math.tan(tmp_radian1) - math.tan(tmp_radian2)) / (1 + math.tan(tmp_radian1) * math.tan(tmp_radian2))
# 答え(少数第2位で表示)
print('(tan60° - tan45°) / (1 + tan60°tan45°) = ', round(result, 2))
■実行結果
▼問題1
tan(165°) = -0.27
(tan120° + tan45°) / (1 - tan120°tan45°) = -0.27▼問題2
tan(15°) = 0.27
(tan60° - tan45°) / (1 + tan60°tan45°) = 0.27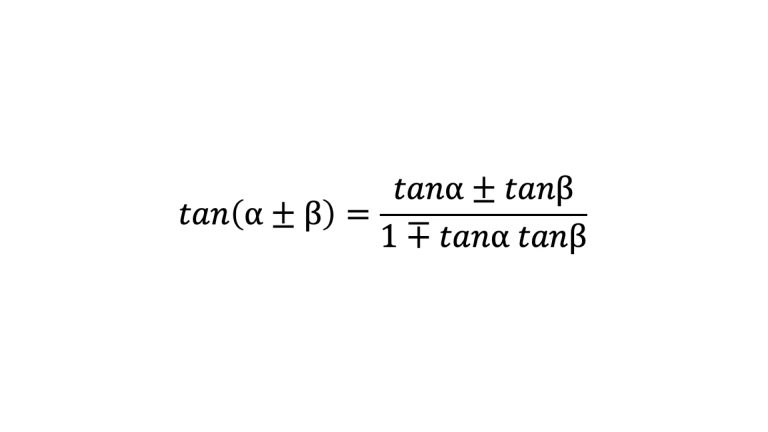

コメント