【Python】sympy.integrateを使用して定積分を解く

■定積分

定積分とは、ある一定の区間[a, b]における、曲線と曲線、曲線と直線とで囲まれた面積である。

・ざっくりイメージ図

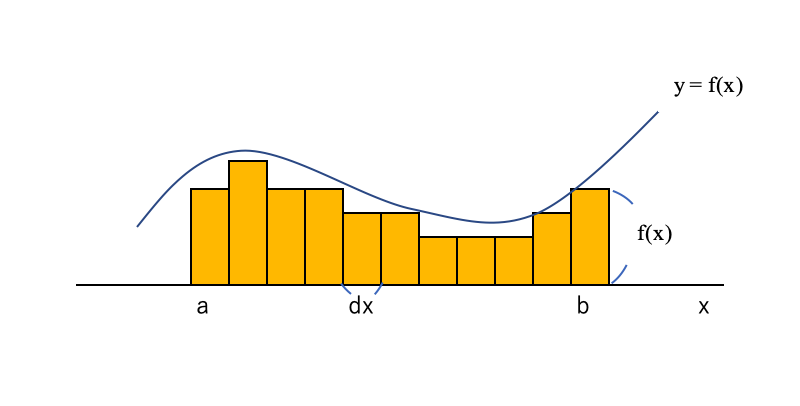
上図の色をつけた長方形について、縦をf(x)とし、横をdxとした場合、長方形の面積は、f(x)とdxを掛け合わせた値「f(x)dx」となる。

dxを限りなく小さい値（ ≒ 0）とし、この長方形を区間[a, b]で加えていけば、面積を求めることができる。

面積Sを求める場合は以下の公式を使用する。

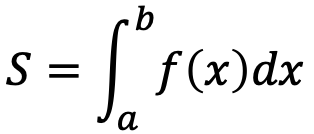
■sympy.integrateの使い方（定積分）

定積分の場合、sympy.integrateは以下のように使用する。

sympy.integrate(計算式, (x, 開始, 終了))

■例題

問題1

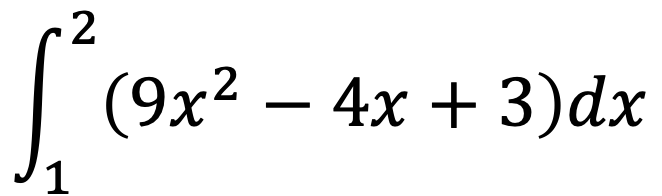
問題2

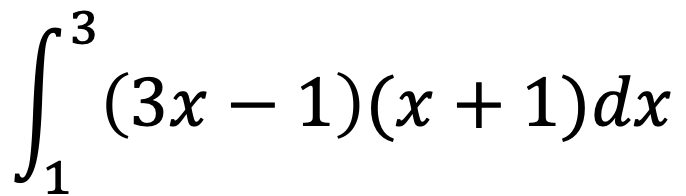
問題3

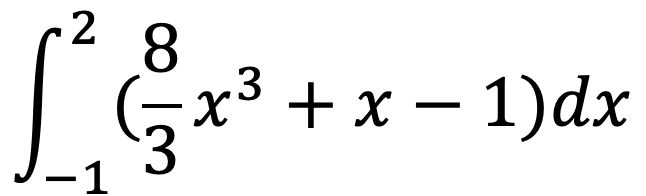
■サンプルコード

import sympy

# 文字列の定義
x = sympy.Symbol('x')

# 問題(1)の式をセット
formula1 = 9 * x ** 2 - 4 * x + 3
# integrateを使用して積分を計算（1から2まで）
ans1 = sympy.integrate(formula1, (x, 1, 2))
# 計算結果を出力
print('問題1：', ans1)

# 問題(2)の式をセット
formula2 = (3 * x - 1) * (x + 1)
# integrateを使用して積分を計算（1から3まで）
ans2 = sympy.integrate(formula2, (x, 1, 3))
# 計算結果を出力
print('問題2：', ans2)

# 問題(3)の式をセット
formula3 = (8 / 3) * x ** 3 + x - 1
# integrateを使用して積分を計算（-1から2まで）
ans3 = sympy.integrate(formula3, (x, -1, 2))
# 計算結果を出力
print('問題3：', round(ans3, 2))

■実行結果

問題1： 18
問題2： 32
問題3： 8.50

■参考

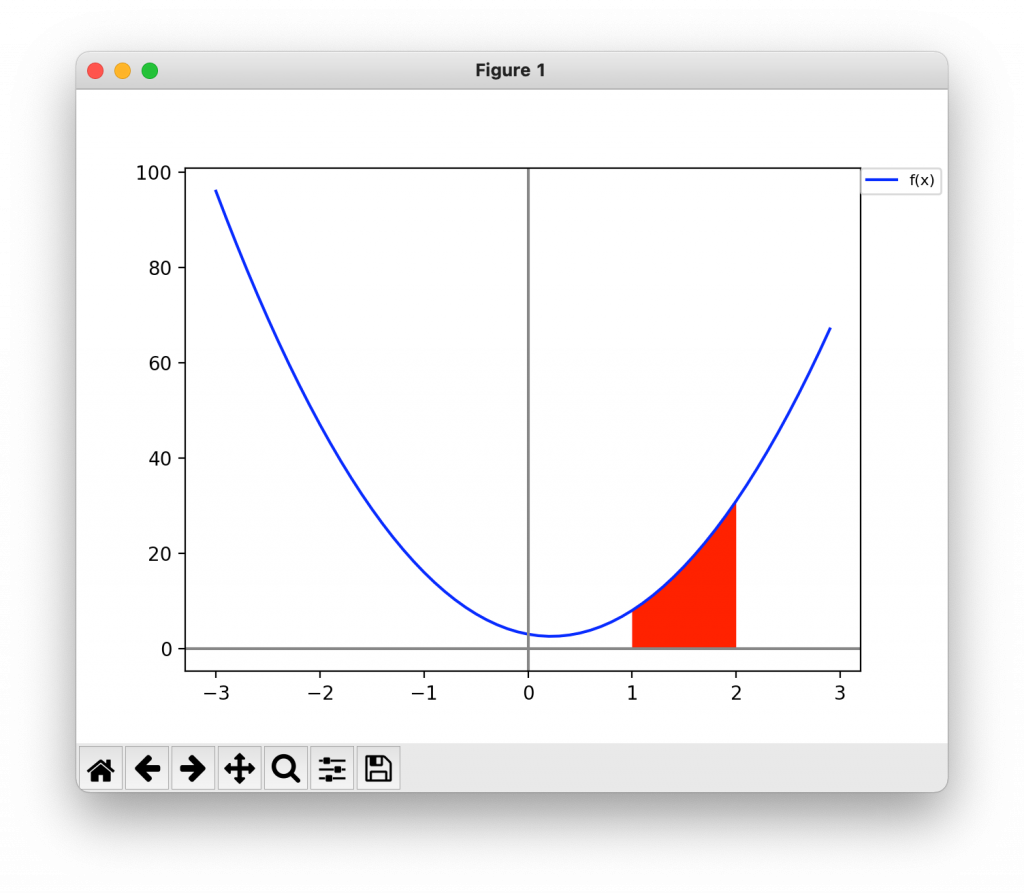
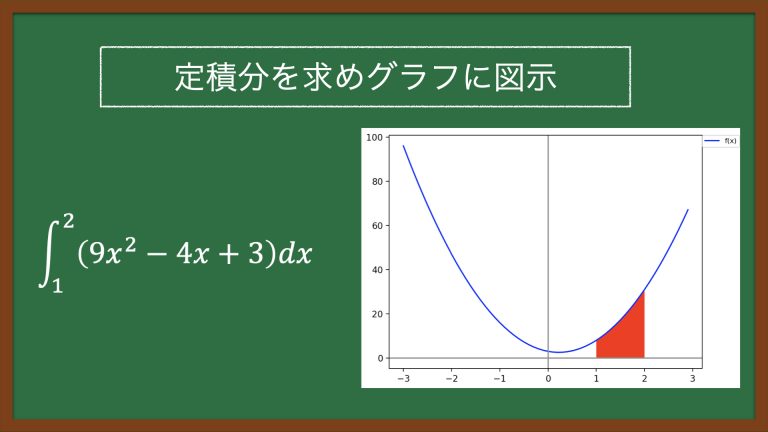
問題1について、面積を求めた部分をグラフに図示し、赤字で示す。

import numpy as np
from matplotlib import pyplot as plt

def MakeGraph():
    # 便宜上、-3から3までの値を0.1間隔で設定
    x_min = -3
    x_max = 3
    x_interval = 0.1
    x_val = np.arange(x_min, x_max, x_interval)

    # 積分の範囲(1から2まで)
    integral_x = np.arange(1, 2.1, 0.1)

    # 関数f(x)を格納する配列
    y_val = []
    integral_y = []

    # それぞれ配列に格納していく(便宜上、nは0.1間隔でセット)
    for i in x_val:
        y_val.append(9 * i ** 2 - 4 * i + 3)

    for i in integral_x:
        integral_y.append(9 * i ** 2 - 4 * i + 3)

    # 関数f(x)のグラフを作成
    plt.plot(x_val, y_val, color='blue', label="f(x)")

    # グラフにx軸,y軸（0）を図示
    # 補助線（0）を作成　[axhline：水平　axvline:垂直]
    plt.axhline(y=0, color="gray")
    plt.axvline(x=0, color="gray")

    # ラベルの表示
    plt.legend(bbox_to_anchor=(1, 1), loc='upper left',
               borderaxespad=0, fontsize=8)

    # xの値が1から2までの範囲を塗りつぶす
    plt.fill_between(integral_x, integral_y, facecolor='red')

    # グラフを表示
    plt.show()


if __name__ == '__main__':
    MakeGraph()