■フィボナッチ数列
2つ前の項と1つ前の項を足し合わせていくことでできる数列である。
▼例
0、1、1、2、3、5、8、13、21、34・・・
▼公式
F0 = 0、F1 = 1
(n ≧ 0)
Fn+2 = Fn+1 + Fn
■例題
▼再帰処理を組み込んだフィボナッチ数列を計算する関数を作成して以下の問題を解く
・問題1
0 ≦ n < 10 の時、Fnの値を求める
・問題2
15番目(n = 15)の時、Fnの値を求める
▼作成するプログラムの概要(フィボナッチ数列を計算する関数)
引数:n(N番目)
①n=0ならば、0を返す。
②n=1ならば、1を返す。
③n=2以上ならば、n-1およびn-2で再び関数を呼び出し(再帰処理)、結果を加算する。
▼フローチャート
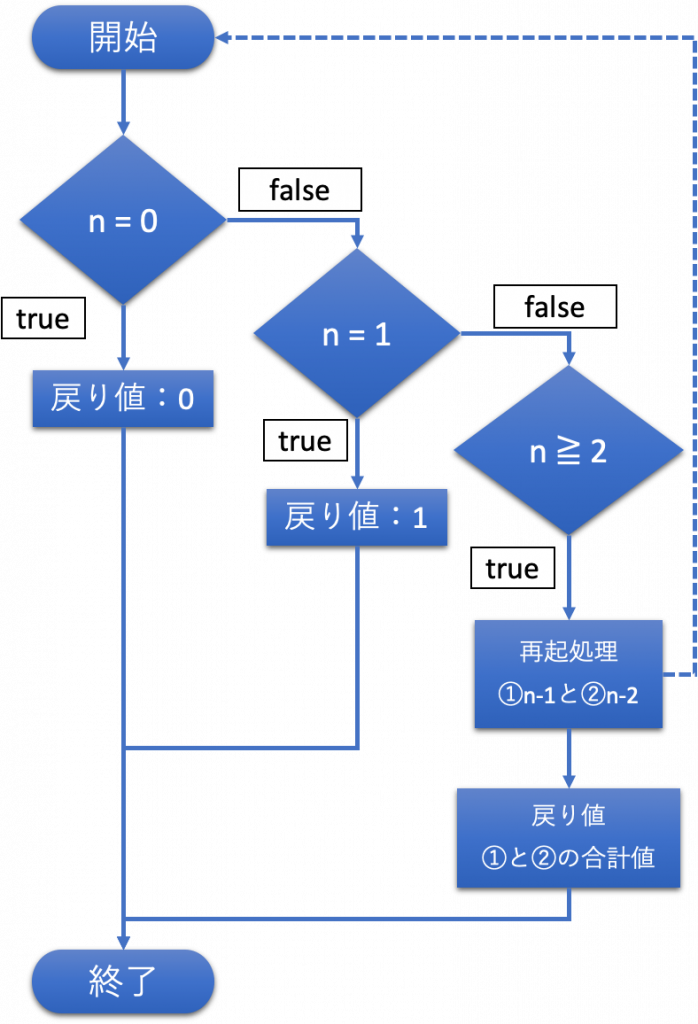
▼補足説明(再帰処理)
n≧2のとき、n-1およびn-2で再び関数を呼び出す処理について、詳細は以下の通りである。
(例)n=2のときの処理概要
上記フローチャート図より、n=2のときは、
①n-1(=1)
②n-2(=0)
の2つの値について再び関数を実行する。
①n=1については、戻り値を1返す。
②n=0については、戻り値を0返す。
したがって、後続処理の①+②(1+0=1)より、戻り値は1となる。
n = 2のとき
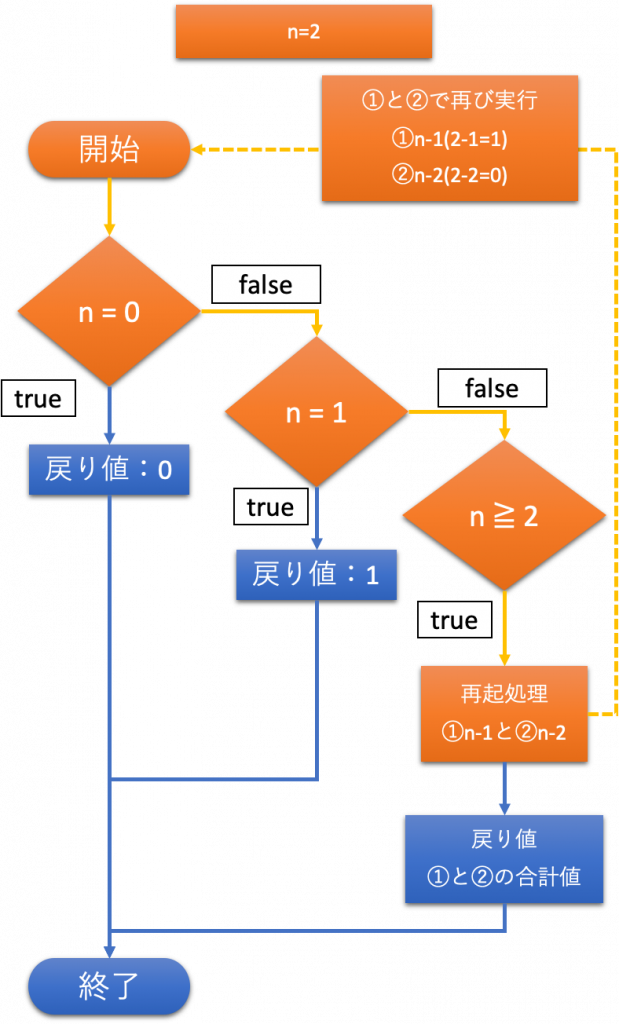
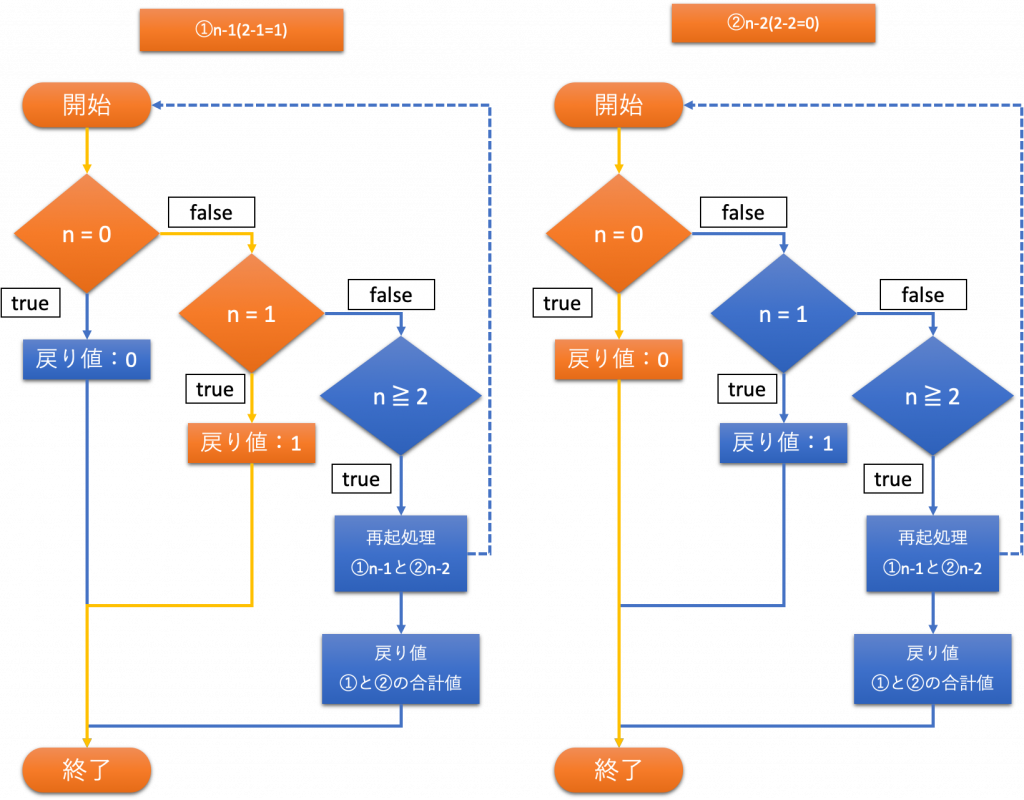
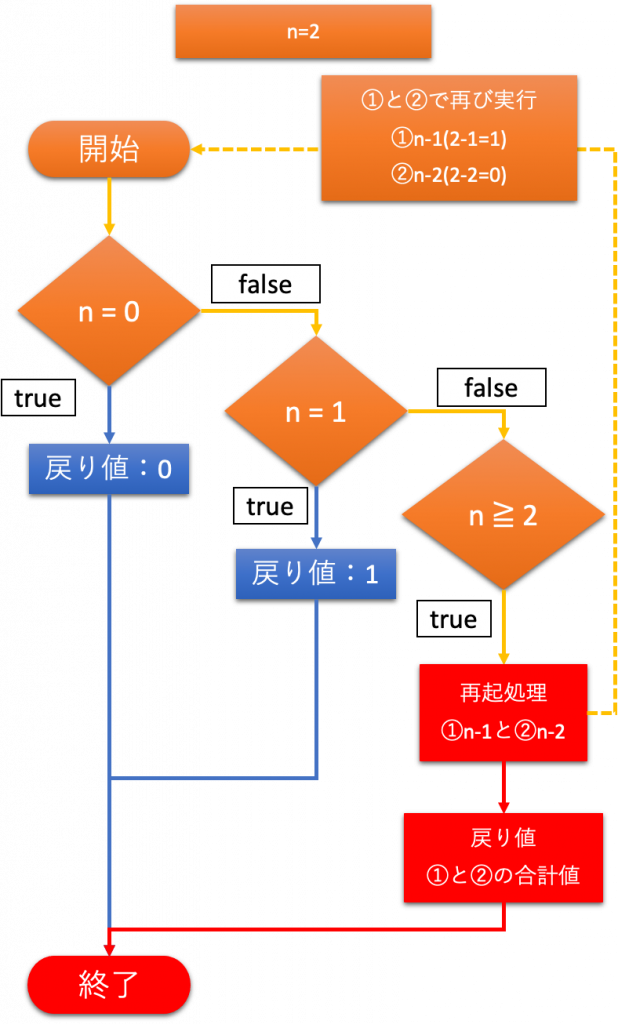
n = 2のとき、計算結果は1である。
■サンプルコード
# -*- Coding: utf-8 -*-
# フィボナッチ数列を計算する関数
# 引数:N番目
# 戻り値:N番目のフィボナッチ数列の値
def FibonacciSeq(n):
# n=0ならば0を返す
if n == 0:
num = 0
# n=1ならば1を返す
elif n == 1:
num = 1
# n=2以上ならばn-1およびn-2で再び関数を呼び出す(再帰処理)
elif n >= 2:
num = FibonacciSeq(n - 1) + FibonacciSeq(n - 2)
return num
# メイン処理
if __name__ == '__main__':
# 問題1
# 結果格納用の配列をセット
ans1= []
# n=0から9まで繰り返したフィボナッチ数列の値をセット
for i in range(10):
ans1.append(FibonacciSeq(i))
# n=0から9まで繰り返したフィボナッチ数列の値を表示する
print('問題1:', ans1)
# 問題2:n=15の時のフィボナッチ数列の値を求める
ans2 = FibonacciSeq(15)
print('問題2:', ans2)
■実行結果
問題1: [0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
問題2: 610