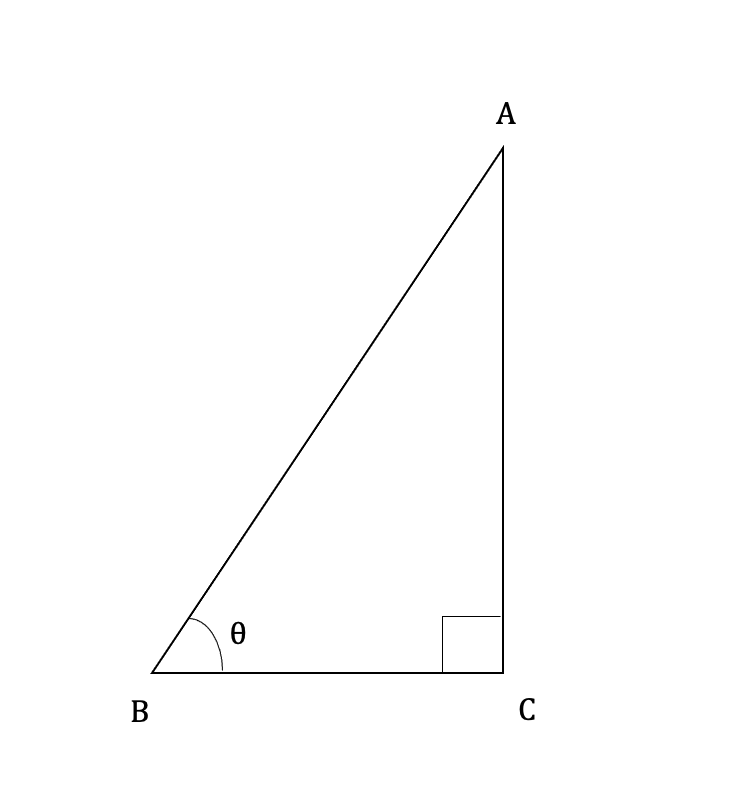
■三角比の定義
直角三角形ABCについてある角度θにおける三角比は以下の通り。
sinθ = AC / AB
cosθ = BC / AB
tanθ = AC / BC
■例題1
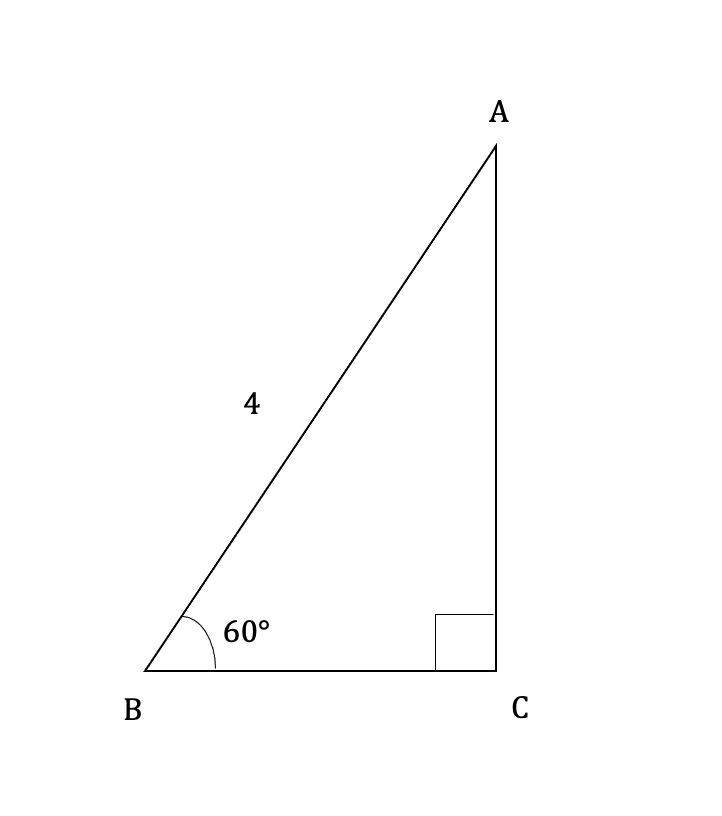
以下の図の直角三角形ABCについて、辺AB = 4、角度B = 60°のとき、
辺ACと辺BCの長さを求める。
▼サンプルコード
辺ACおよび辺BCは以下の式で求めることができる。
辺AC = 辺AB × sin60°
辺BC = 辺AB × cos60°
Pythonのmath.sin()、math.cos()を使用する場合の引数は、ラジアン(弧度法)であることに注意!!
# -*- Coding:UTF-8 -*-
import math
# 辺ABの長さを変数に格納
AB = 4
# 60度(度数法)をラジアン(弧度法)に変換
radian60 = math.radians(60)
# sin60°とcos60°を求める
sin60 = math.sin(radian60)
cos60 = math.cos(radian60)
# 辺ACを算出
AC = AB * sin60
# 辺BCを算出
BC = AB * cos60
# 計算結果を表示(便宜上少数第2位まで)
print('AC = ', round(AC, 2))
print('BC = ', round(BC, 2))
▼実行結果
AC = 3.46
BC = 2.0■例題2
以下の直角三角形ABCについて、辺BC=3、角度B=76°のとき、辺ABおよび辺ACを求める。

▼サンプルコード
辺ABおよび辺ACは以下の式で求めることができる。
辺AB = 辺BC ÷ cos76°
辺AC = 辺BC × tan76°
Pythonのmath.cos()、math.tan()を使用する場合の引数は、ラジアン(弧度法)であることに注意!!
# -*- Coding:UTF-8 -*-
import math
# 辺BCの長さを変数に格納
BC = 3
# 76度(度数法)をラジアン(弧度法)に変換
radian76 = math.radians(76)
# cos76°とtan76°を求める
cos76 = math.cos(radian76)
tan76 = math.tan(radian76)
# 辺ABを算出
AB = BC / cos76
# 辺ACを算出
AC = BC * tan76
# 計算結果を表示(便宜上少数第2位まで)
print('AB = ', round(AB, 2))
print('AC = ', round(AC, 2))
▼実行結果
AB = 12.4
AC = 12.03