【Python】等比数列の和の公式を使って問題を解く / え〜のう

■等比数列の和の公式
■例題
■サンプルコード
■実行結果

■等比数列の和の公式

初項a、公比r、項数nの等比数列の和S_nは以下のように表す。

▼ r = 1 の場合（公式①）

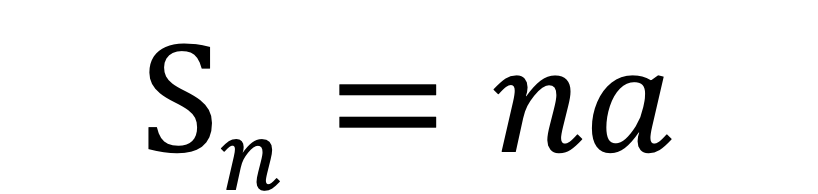
▼ r < 1 の場合（公式②）

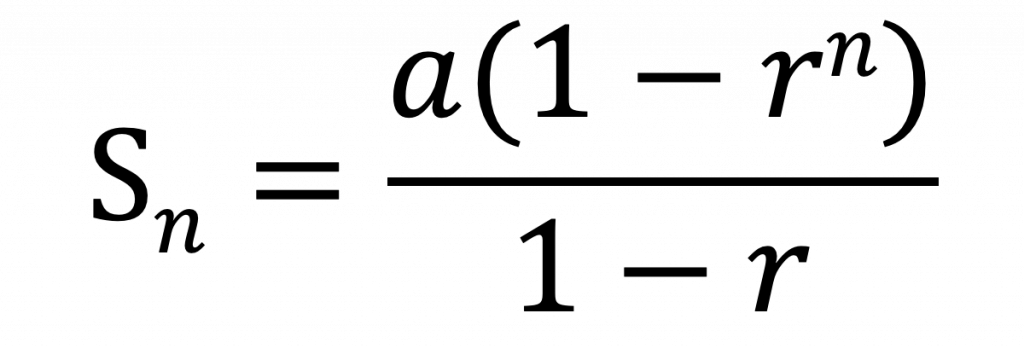
▼ r > 1 の場合（公式③）

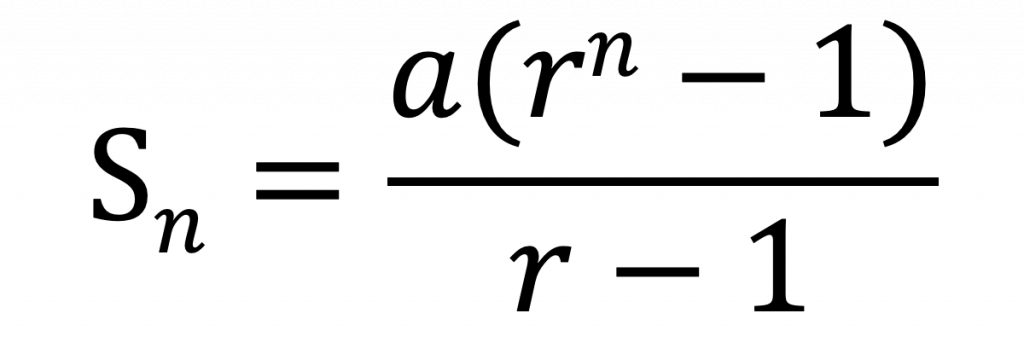
※補足
r > 1 のとき、公式②を使用しても、分母・分子がマイナスになるだけなので公式②＝公式③が成り立つ。

（例）初項2、公比3、第4項までの等比数列の和を求める。

（1）公式②を使用する場合・・・

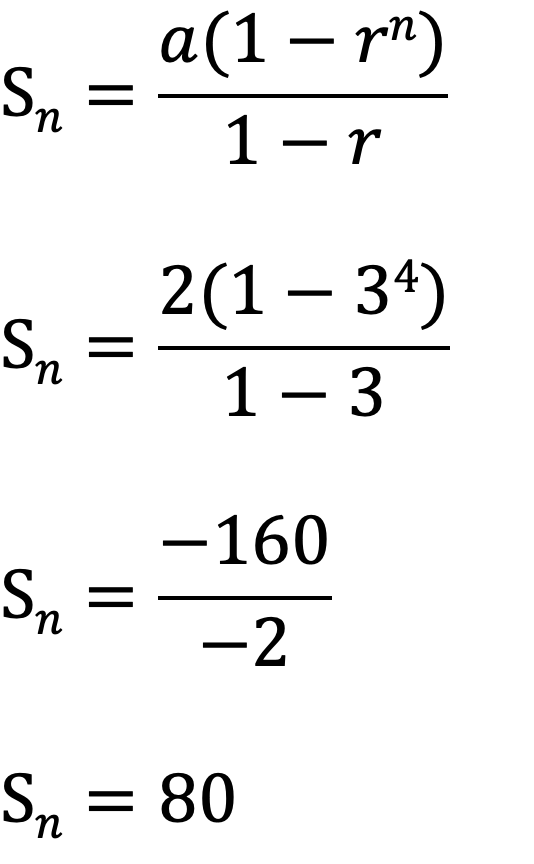
（2）公式③を使用する場合・・・

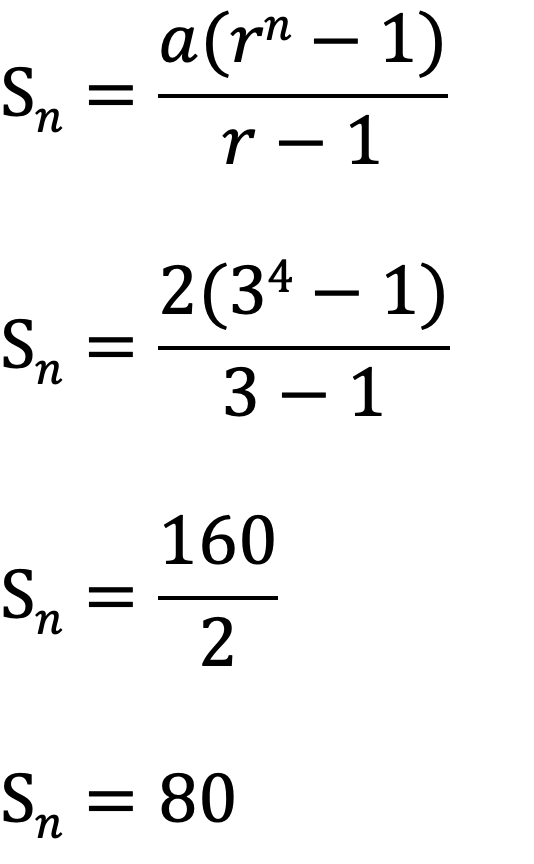
▼参考（等比数列についての参照先）

【Python】等比数列：1からN番目までの値（項）を表示する

■等比数列等差数列とは、隣り合う2項の比が一定の数列である。（例）2、4、8、16、32、64、128 ・・・・・・①上記（例：①の数列）について、ひとつひとつの値を「項」と呼び、最初の項を「初項」、隣り合う2項の比を「公比」と呼ぶ。したが...

■例題

以下の問題について等比数列の和を求める。

問題1
初項：4、公比：1、第7項までの等比数列の和

問題2
初項：7、公比：-3、第5項までの等比数列の和

問題3
初項：2、公比：3、第10項までの等比数列の和

■サンプルコード

# -*- Coding:UTF-8 -*-

def SumTohiSuretsu(a:int, r:int, n:int) -> float:
    # 合計の初期値をセット
    sum = 0

    # rについて、1、1より小さい、1より大きいで条件分岐
    if r == 1:
        # 公式①
        sum = a * n
    elif r < 1:
        # 公式②
        sum = (a * (1 - (r ** n))) / (1 - r)
    elif r > 1:
        # 公式③
        sum = (a * ((r ** n) - 1)) / (r - 1)


    return sum

if __name__ == '__main__':
    # 問題1　初項：4、公比：1、第7項までの等比数列の和
    a1 = 4
    r1 = 1
    n1 = 7

    print(SumTohiSuretsu(a1, r1, n1))

    # 問題2　初項：7、公比：-3、第5項までの等比数列の和
    a2 = 7
    r2 = -3
    n2 = 5

    print(SumTohiSuretsu(a2, r2, n2))

    # 問題3　初項：2、公比：3、第10項までの等比数列の和
    a3 = 2
    r3 = 3
    n3 = 10

    print(SumTohiSuretsu(a3, r3, n3))