■極値
関数f(x) = x3 -3x + 1について、導関数f'(x)を求める。
f'(x) = 3x2 – 3
f'(x) = 3(x2 – 1)
f'(x) = 3(x – 1)(x + 1)
すなわち、x = -1、1のとき、導関数f'(x)の値は0になる。
以下に関数f(x)および導関数f'(x)について、増減表を作成する。
| x | ・・・ | -1 | ・・・ | 1 | ・・・ |
| f'(x) | + | 0 | ー | 0 | + |
| f(x) | ↗︎ | 極大値 | ↘︎ | 極小値 | ↗︎ |
導関数f'(x) = 0のとき、関数f(x)の値を極値(極大値・極小値)と呼ぶ。
■例題
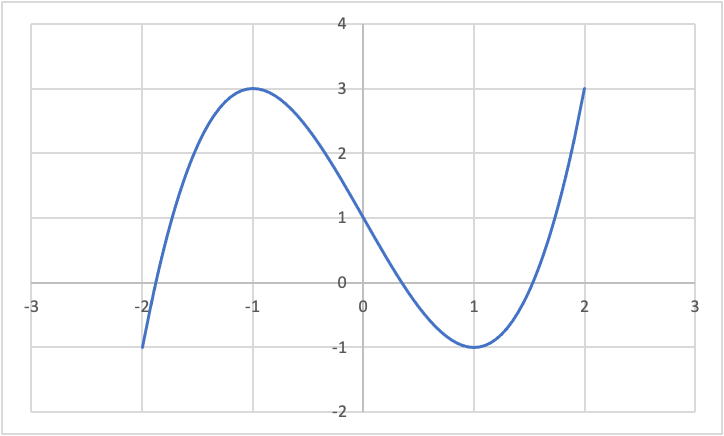
次の関数f(x)について、極値を求め、グラフに図示する。
(1)f(x) = x3 -3x + 1
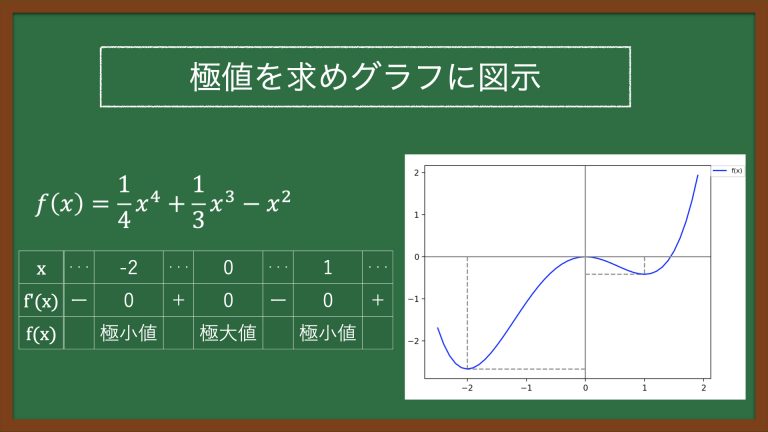
(2)f(x) = (1/4)x4 + (1/3)x3 – x2
■サンプルコード
import sympy
import numpy as np
from matplotlib import pyplot as plt
# 微分する関数
def f_diff(y):
return sympy.diff(y)
# 極値を求める関数
def cal_extremum(y_diff):
# 微分の結果から極値を求める
return sympy.solve(y_diff)
def MakeGraph(y, extremum):
# 便宜上、-2.5から2までの値を0.1間隔で設定
x_min = -2.5
x_max = 2
x_interval = 0.1
x_val = np.arange(x_min, x_max, x_interval)
# 関数f(x)を格納する配列
y_val = []
# それぞれ配列に格納していく(便宜上、nは0.1間隔でセット)
for i in range(len(x_val)):
y_val.append(y.subs(x, x_val[i]))
# 関数f(x)のグラフを作成
plt.plot(x_val, y_val, color='blue', label="f(x)")
# グラフにx軸,y軸(0)を図示
# 補助線(0)を作成 [axhline:水平 axvline:垂直]
plt.axhline(y=0, color="gray")
plt.axvline(x=0, color="gray")
# x軸・y軸から極値までを点線で作成
for j in range(len(extremum)):
# 極値を一時変数に格納
tmp_x = float(extremum[j])
# y の値を一時変数に格納
tmp_y = float(y.subs(x, tmp_x))
# 補助線を点線で作成 [hlines:水平 vlines:垂直]
plt.hlines([tmp_y], 0, tmp_x, "gray", linestyles='dashed')
plt.vlines([tmp_x], 0, tmp_y, "gray", linestyles='dashed')
# ラベルの表示
plt.legend(bbox_to_anchor=(1, 1), loc='upper left',
borderaxespad=0, fontsize=8)
# グラフを表示
plt.show()
if __name__ == '__main__':
# 文字列を設定
x = sympy.Symbol('x')
# 問題1 f(x)=x**3 - 3x + 1
y1 = x ** 3 - 3 * x + 1
# 微分する
y1_diff = f_diff(y1)
# 極値(xの値)を求める
extremum_1 = cal_extremum(y1_diff)
# 極値を出力
print('問題1の極値')
for i in range(len(extremum_1)):
print('x = ', extremum_1[i])
print('f(x) = ', y1.subs(x, extremum_1[i]))
# グラフ作成
MakeGraph(y1, extremum_1)
# 問題2 f(x)=(1/4)x**4 + (1/3)x**3 - x**2
y2 = (1/4) * x ** 4 + (1/3) * x ** 3 - x ** 2
# 微分する
y2_diff = f_diff(y2)
# 極値(xの値)を求める
extremum_2 = cal_extremum(y2_diff)
# 極値を出力
print('問題2の極値')
for i in range(len(extremum_2)):
print('x = ', round(extremum_2[i]))
print('f(x) = ', round(y2.subs(x, extremum_2[i]), 2))
# グラフ作成
MakeGraph(y2, extremum_2)
■実行結果
(1)f(x) = x3 -3x + 1
問題1の極値
x = -1
f(x) = 3
x = 1
f(x) = -1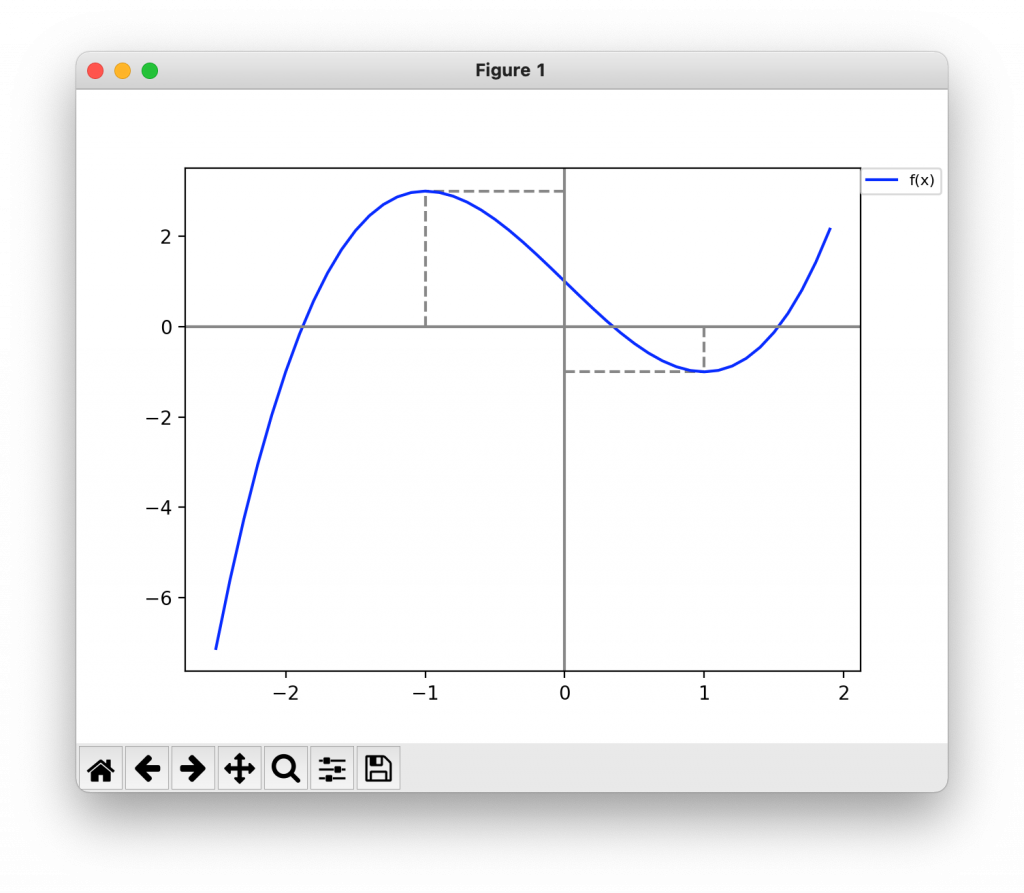
(2)f(x) = (1/4)x4 + (1/3)x3 – x2
問題2の極値
x = -2
f(x) = -2.67
x = 0
f(x) = 0
x = 1
f(x) = -0.42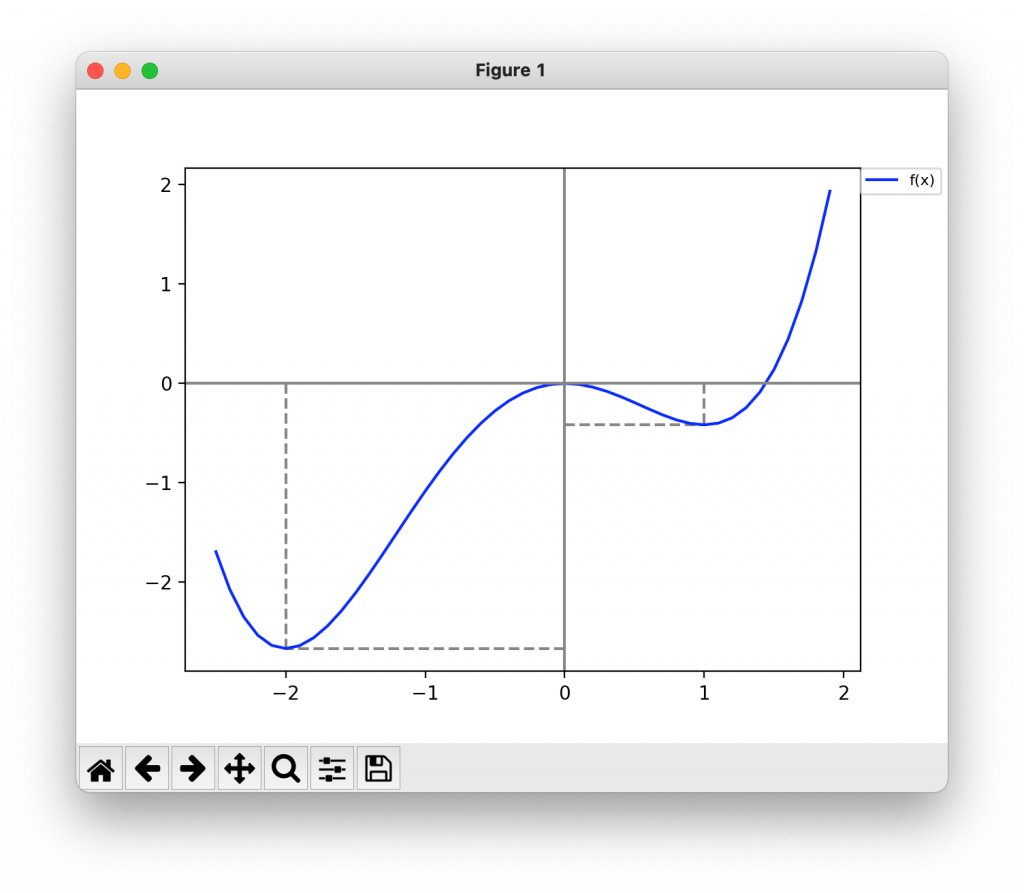
コメント