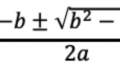【Python】 1次関数　2点から傾きと切片を求めてグラフに表示

■1次関数

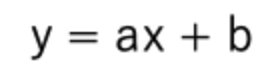
a：傾き（変化の割合）
b：切片

a > 0 の時、グラフは右上がり

a < 0 の時、グラフは右下がり

ある直線上の2点、A(x1, y1)およびB(x2, y2)より、
傾き（変化の割合）および切片は以下の通り算出する

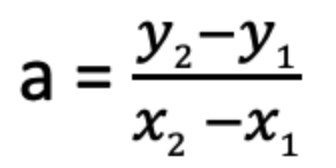
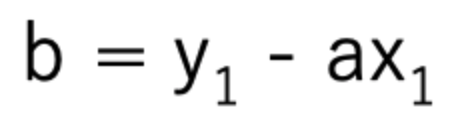
※切片を求める時は（x2, y2）を使用しても可

■例題

(1)2点(1, 7), (3, 13) の1次関数をグラフで図示。

(2)2点(1, 1), (6, -9) の1次関数をグラフで図示。

■サンプルコード

# -*- Coding: UTF-8 -*-
import numpy as np
from matplotlib import pyplot as plt

# 傾きと切片を算出する関数
# 引数     ：座標(x1, y1)と座標(x2, y2)
# 戻り値   ：配列[傾き, 切片]
def LinearFunc(x1: int, y1: int, x2: int, y2: int) -> list:
    # 変数宣言（戻り値用の配列）
    result_data = []

    # 傾きを求める
    a = (y2 - y1) / (x2 - x1)

    # 傾きを配列にセット
    result_data.append(a)

    # 切片を求める
    b = y1 - a * x1

    # 切片を配列にセット
    result_data.append(b)

    return result_data

# グラフを作成する関数
# 引数   ：配列[傾き, 切片]
def MakeGraph(data: list):
    # 傾き（ a ）と切片（ b ）を変数にセット
    a = data[0]
    b = data[1]


    # 便宜上、0.1間隔で　-10 < x < 10 の範囲を指定
    xmin = -10
    xmax = 10
    xinterval = 0.1
    x = np.arange(xmin, xmax, xinterval)

    # yを算出
    y = a * x + b

    # yの最小・最大インデックスを取得
    y_minindex = np.argmin(y)
    y_maxindex = np.argmax(y)

    # yの最小・最大値を取得
    ymin = y[y_minindex]
    ymax = y[y_maxindex]

    # グラフを作成
    plt.plot(x,y)

    # x軸とy軸の範囲を設定
    plt.xlim(xmin, xmax)
    plt.ylim(ymin, ymax)

    # 補助線（0）を点線で作成　[hlines：水平　vlines:垂直]
    plt.hlines([0], xmin, xmax, "gray", linestyles='dashed')
    plt.vlines([0], ymin, ymax, "gray", linestyles='dashed')

    # グラフを表示
    plt.show()


# メイン処理
if __name__ == '__main__':
    # (1)2点(1, 7), (3, 13) の1次関数を求める。
    x1 = 1
    y1 = 7
    x2 = 3
    y2 = 13

    # 傾き・切片を求める
    data = LinearFunc(x1, y1, x2, y2)
    print('傾き：' + str(data[0]))
    print('切片：' + str(data[1]))

    # グラフの作成
    MakeGraph(data)

    # (2)2点(1, 1), (6, -9) の1次関数を求める。
    x1 = 1
    y1 = 1
    x2 = 6
    y2 = -9

    # 傾き・切片を求める
    data = LinearFunc(x1, y1, x2, y2)
    print('傾き：' + str(data[0]))
    print('切片：' + str(data[1]))

    # グラフの作成
    MakeGraph(data)

■実行結果

(1)2点(1, 7), (3, 13) の1次関数をグラフで図示。

傾き：3.0
切片：4.0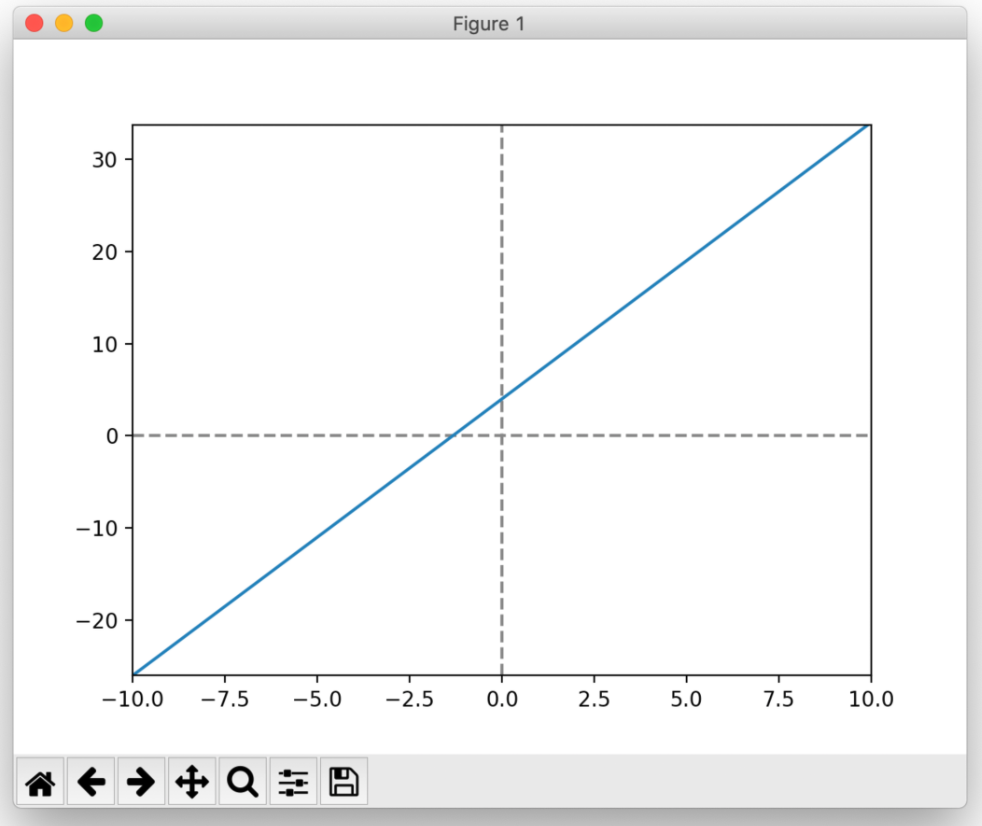

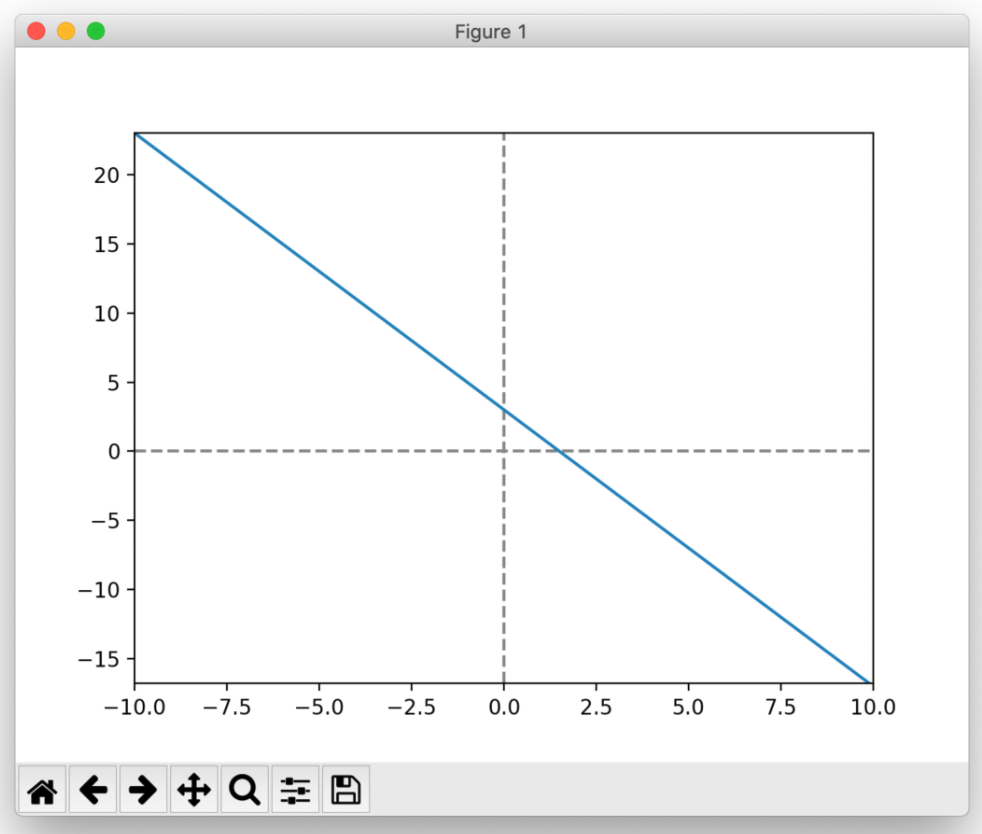
(2)2点(1, 1), (6, -9) の1次関数をグラフで図示。

傾き：-2.0
切片：3.0