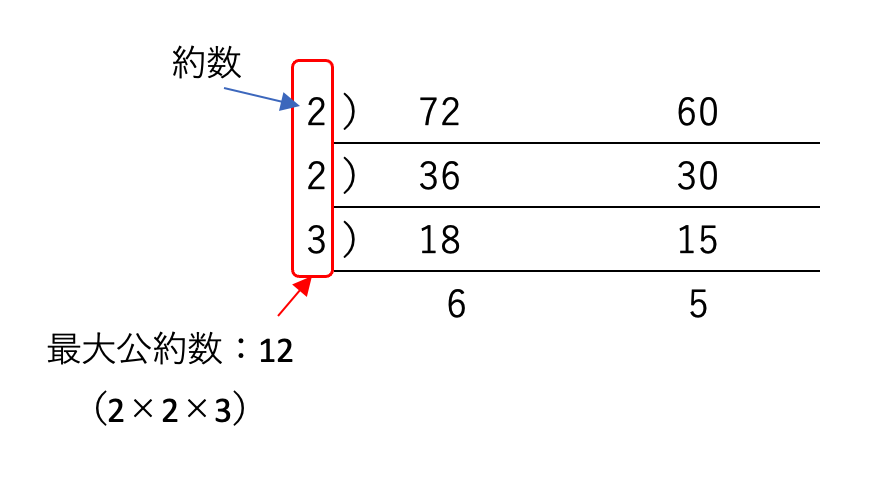
■最大公約数とは
最大公約数とは、2つ以上の正の整数に共通な約数(公約数)のうち最大のものを言う。
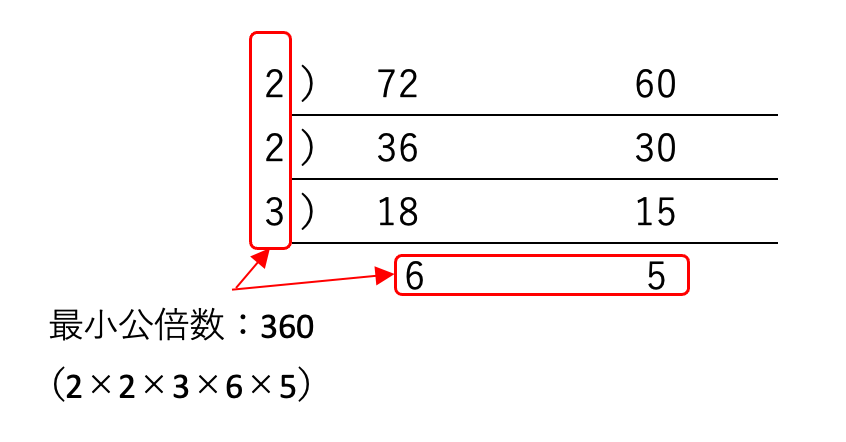
■最小公倍数とは
最小公倍数とは、2つ以上の正の整数の共通な倍数(公倍数)のうち最小のものを言う。
■作成するプログラムの仕様
▼処理概要
【メイン処理】
①変数(a、b)に任意の整数をセット(今回は60と72)。
②最大公約数算出関数 gcf()を呼び出し、結果を出力する。
③最小公倍数算出関数 lcm()を呼び出し、結果を出力する。
【最大公約数算出関数 gcf()】※1
[引数]a:任意の整数(int)、b:任意の整数(int)
[戻り値]a:最大公約数
①引数a = bになるまでループ処理を繰り返す。
①-1.a > bならば、a = a – b
①-2.a < bならば、b = b – a
②最大公約数[a]を返す。
【最小公倍数算出関数 lcm()】※2
[引数]a:任意の整数(int)、b:任意の整数(int)
[戻り値]最小公倍数
① [a × b ÷ aとbの最大公約数] を返す。
▼補足説明
※1【最大公約数算出関数 gcf()】について
ある2つの正の整数について、[大きい数]-[小さい]を繰り返すと、最終的に等しくなり、
等しくなった数が最大公約数となる。
(例)a = 72、b = 60 の場合
a(72) > b(60) → a = a(72) – b(60) = 12
a(12) < b(60) → b = b(60) – a(12) = 48
a(12) < b(48) → b = b(48) – a(12) = 36
a(12) < b(36) → b = b(36) – a(12) = 24
a(12) < b(24) → b = b(24) – a(12) = 12
a(12) = b(12)
終了(最大公約数:12)
※2【最小公倍数算出関数 lcm()】について
ある2つの正の整数をかけて最大公約数で割ると最小公倍数が算出できる。
例)a = 72、b = 60 の場合
a(72) × b(60) / 最大公約数(12) = 360
▼フローチャート
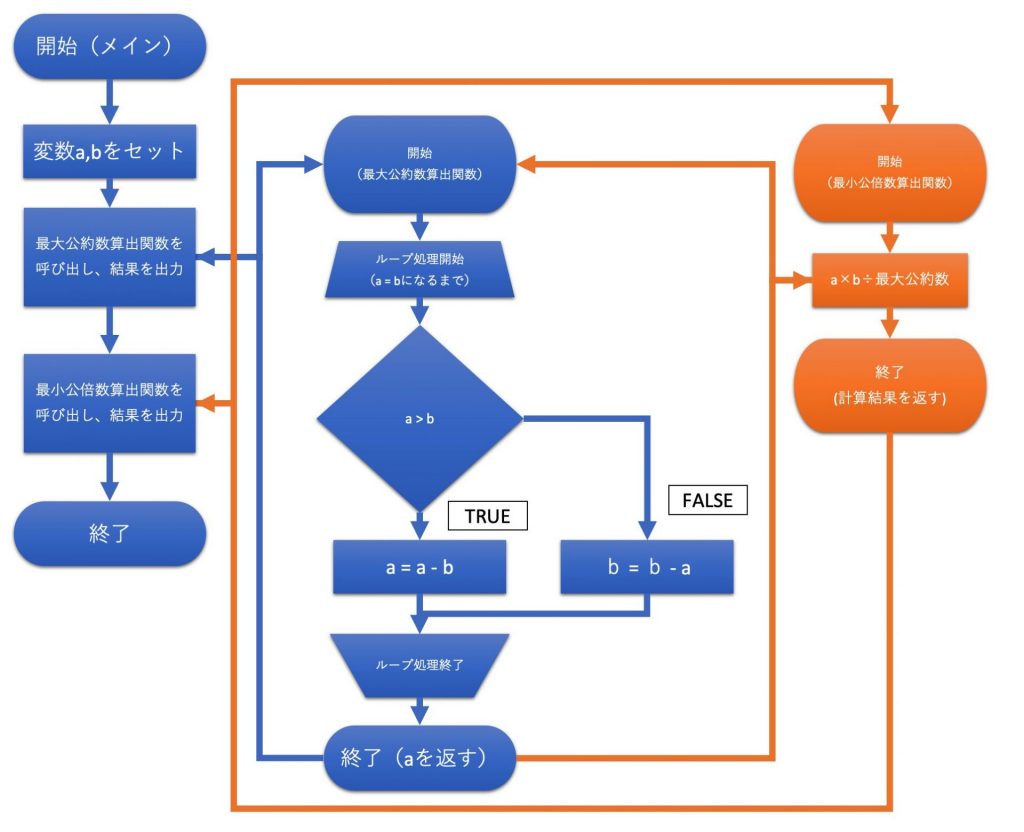
■サンプルコード
public class Sample{
// 最大公約数を算出する関数
// [引数]a:任意の整数(int)、b:任意の整数(int)
// [戻り値]a:最大公約数
private static int gcf(int a, int b) {
// ユークリッド互除法にて最大公倍数を算出
while(a!=b) {
if(a>b) {
a -= b;
}else {
b -= a;
}
}
return a;
}
// 最小公倍数を算出する関数
// [引数]a:任意の整数(int)、b:任意の整数(int)
// [戻り値]最小公倍数
private static int lcm(int a, int b) {
return a * b / gcf(a, b);
}
// メイン処理
public static void main(String[] args) {
// 任意の整数をセット
int a = 60;
int b = 72;
// gcf()を呼び出し、結果を出力
System.out.println("最大公約数:" + gcf(a, b));
// lcm()を呼び出し、結果を出力
System.out.println("最小公倍数:" + lcm(a, b));
}
}
■実行結果
最大公約数:12
最小公倍数:360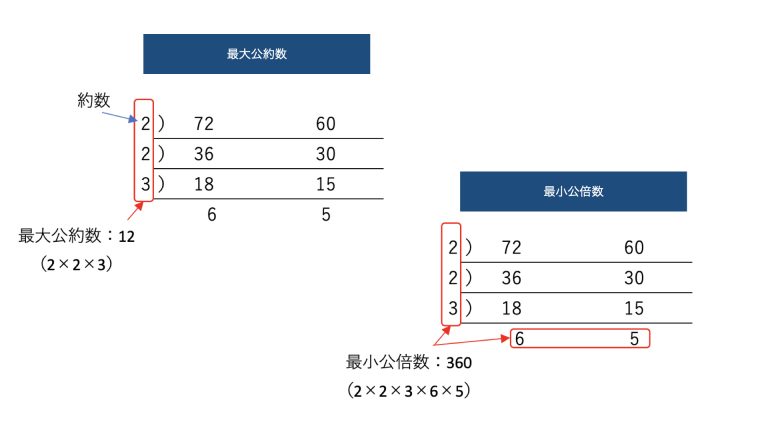

コメント