■三角方程式
三角方程式は、基本的に単位円(0≦x≦2πの範囲)における、ある角度(x:ラジアン表記)を含む三角関数の方程式を言う。
■例題
0≦x≦2πのとき、次の方程式を解く。
▼問題1
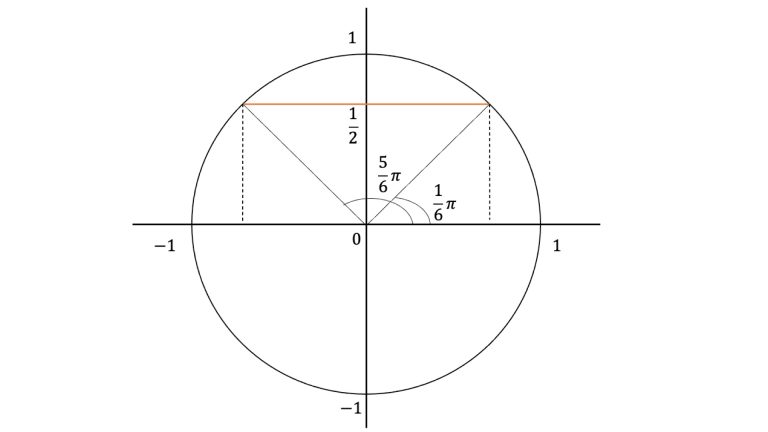
2sinx – 1 = 0
▼問題2
cos2x + cosx = 0
■使用するライブラリ
▼importするライブラリ
sympy
| 使用するメソッド | 説明 |
|---|---|
| sympy.Symbol(‘x’) | 計算式に文字列をセットする |
| sympy.solve(計算式, 任意の文字) | 任意の文字について方程式を解く |
| sympy.pi | πラジアン |
| sympy.sin() | 三角関数のsin |
| sympy.cos() | 三角関数のcos |
■サンプルコード
# -*- Coding:UTF-8 -*-
import sympy
# 0≦x≦2πの範囲の値のみを配列に格納する関数
# 引数:配列
# 戻り値:配列
def ZeroTo2Pi(ans:list) -> list:
# 戻り値用の配列をセット
result = []
# πラジアンをセット
pi = sympy.pi
# 引数の配列分、ループ処理を行う
for i in range(len(ans)):
# 配列の要素が0以上かつ2π以下の結果のみを戻り値用の配列に格納する
if ans[i] >= 0 and ans[i] <= 2 * pi:
result.append(ans[i])
return result
if __name__ == '__main__':
# 文字列をセット
x = sympy.Symbol('x')
# 問題1:2sinx - 1 = 0
ans1 = sympy.solve(2 * sympy.sin(x) - 1, x)
print('計算結果(全量):', ans1)
print('計算結果(0≦x≦2π):', ZeroTo2Pi(ans1))
# 問題2:cos2x + cosx = 0
ans2 = sympy.solve(sympy.cos(2 * x) + sympy.cos(x), x)
print('計算結果(全量):', ans2)
print('計算結果(0≦x≦2π):', ZeroTo2Pi(ans2))
■実行結果
▼問題1
計算結果(全量): [pi/6, 5*pi/6]
計算結果(0≦x≦2π): [pi/6, 5*pi/6]▼問題2
計算結果(全量): [-5*pi/3, -pi, -pi/3, pi/3, pi, 5*pi/3]
計算結果(0≦x≦2π): [pi/3, pi, 5*pi/3]※補足事項
piはπラジアンを示す