【Python】Σ（シグマ）：自然数の累乗の和の公式を使って問題を解く / え〜のう

■シグマの表記方法
■自然数の累乗の和の公式
■例題
■サンプルコード
■実行結果

■シグマの表記方法

自然数の累乗の和の公式を使用する際、Σ（シグマ）を使用してまとめることができる。
例えば、1から10までの和（＝1＋2＋3＋4＋・・・＋9＋10）をΣ（シグマ）を使用して表す場合は、以下の通りとなる。

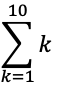
これは、kに1から10までの自然数をすべて加算するという表記となる。
また、このシグマの式は、初項1、公差1の等差数列を第10項まで加算するという意味にもなる。

▼等差数列についての参照先

■等差数列等差数列とは、隣り合う2項の差が一定の数列である。（例）1、4、7、10、13、16、19 ・・・・・・①上記（例：①の数列）について、ひとつひとつの値を「項」と呼び、最初の項を「初項」、隣り合う2項の差を「公差」と呼ぶ。したがっ...

【Python】等差数列の和の公式を使って問題を解く

■等差数列の和の公式初項：a , 公差：d ,項数：n ,末項：l のとき、等差数列の和Snは、以下のように求めることができる。※等差数列についての参照先。■例題（1）初項2、公差3、項数17の等差数列の和を求める。（2）初項10、末項-3...

■自然数の累乗の和の公式

前項のΣ（シグマ）を使用した累乗の和について、以下の公式が成り立つ。

①自然数の累乗の和の公式

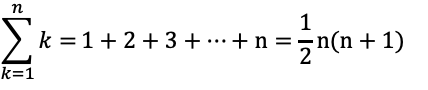
②自然数の累乗の和の公式（2乗）

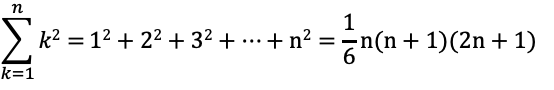
③自然数の累乗の和の公式（3乗）

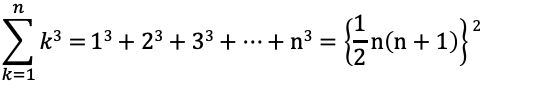
■例題

以下の4問について、自然数の累乗の和の公式を使用して問題を解く。

問題1

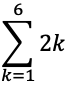
問題2

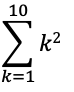
問題3

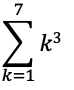
問題4

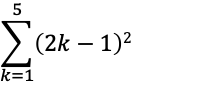
■サンプルコード

# -*- Coding:UTF-8 -*-

# 自然数の累乗の和の公式
# 引数：n項
# 戻り値：自然数の累乗の和
def func_ruijo(n:int):

    # Σ K(n, k=1) = 1/2n(n+1)
    ans = (1 / 2) * n * (n + 1)

    # 計算結果を戻り値として返す。
    return ans

# 自然数の累乗の和の公式（2乗）
# 引数：n項
# 戻り値：自然数の累乗の和（2乗）
def func_ruijo_2(n:int):
    # Σ K**2(n, k=1) = 1/6n(n+1)(2n+1)
    ans = (1 / 6) * n * (n + 1) * (2 * n + 1)

    # 計算結果を戻り値として返す。
    return ans

# 自然数の累乗の和の公式（3乗）
# 引数：n項
# 戻り値：自然数の累乗の和（3乗）
def func_ruijo_3(n:int):
    # Σ K**3(n, k=1)
    ans = ((1 / 2) * n * (n + 1)) ** 2

    # 計算結果を戻り値として返す。
    return ans


# メイン処理
if __name__ == '__main__':
    # 問題1：Σ 2K(n=6, k=1)
    ans1 = 2 * (func_ruijo(6))
    print('問題1：', ans1)

    #問題2：Σ K**2(n=10, k=1)
    ans2 = func_ruijo_2(10)
    print('問題2：', ans2)

    #問題2：Σ K**3(n=7, k=1)
    ans3 = func_ruijo_3(7)
    print('問題3：', ans3)

    # 問題4：Σ (2K-1)**2(n=5, k=1) = Σ (4k**2 - 4K + 1)(n=5, k=1)
    ans4 = (4 * func_ruijo_2(5)) - (4 * func_ruijo(5)) + 5
    print('問題4：', ans4)

問題1について

以下の通り、kを2倍する場合は、それぞれの値を2倍しながら足していくのも、全てを足してから（kの値を算出してから）2倍しても答えは同じになるため、後者の全てを足してから（kの値を算出してから）2倍する方針とする。

▼イメージ

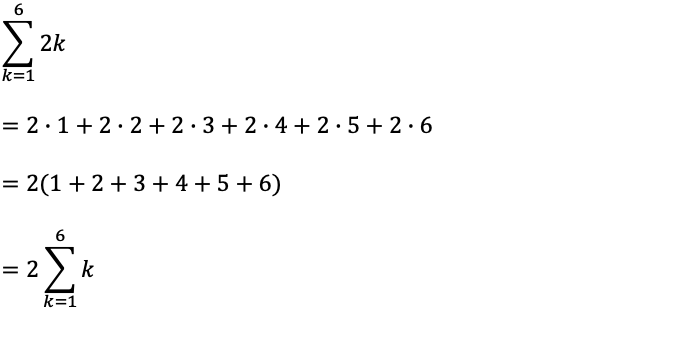
問題4について

(2k-1)²を展開し、（4k² – 4K + 1）の状態とする。
その後に、（4k² – 4K + 1）について、それぞれ計算を行なっていく。

▼イメージ

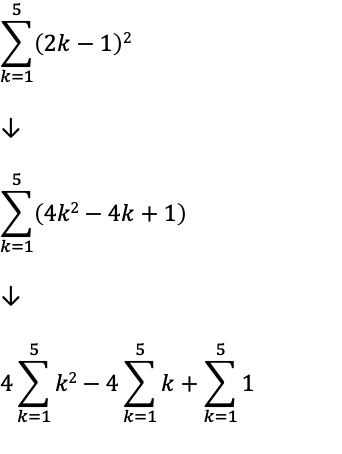
▼問題4の補足

以下のkを含まない式は、1を5回足す（=5）となる。

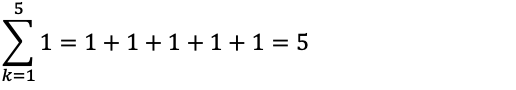
■実行結果

問題1： 42.0
問題2： 385.0
問題3： 784.0
問題4： 165.0