■分数数列
分数数列とは、分母が一定の割合で増減していく数列である。

■部分分数分解
分数数列の和を求める際は、分母の値を2つ数以上の分数の和や差に変形して求める(部分分数分解)。
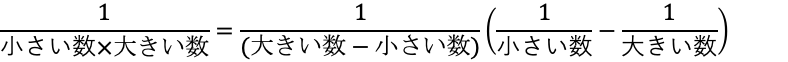
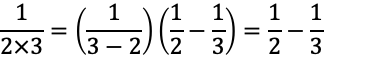
■分数数列の和の求め方(机上計算)
次の分数数列のについて、第10項までの和を求める。
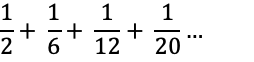
▼スッテプ1:第k項の値を求める。
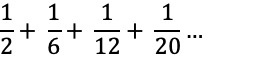
↓規則性を調べるために、とりあえず、分母を2で因数分解してみる。
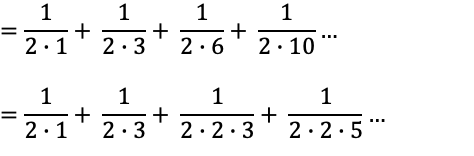
↓各分母について、n番目の値とn+1番目の値を掛け合わせていることがわかる。
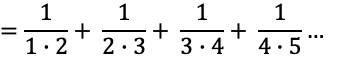
したがって、第k項の値は、以下の通り。
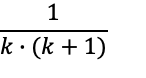
▼ステップ2:シグマ(Σ)に値をセットして、計算する。
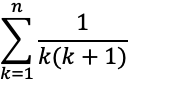
↓部分分数分解を使用する。
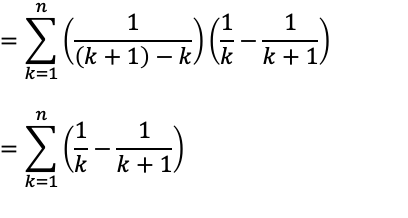
↓シグマ(Σ)の計算:1からnまでの和を求める。
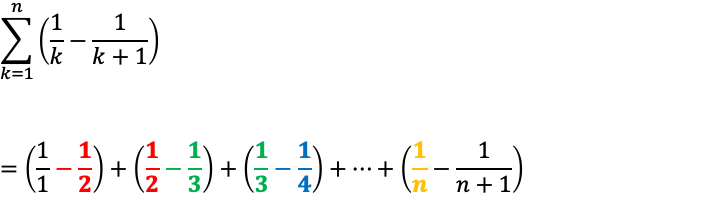
シグマの計算をしていくと、それぞれ同じ色の部分同士で相殺され0になっていく。
したがって、求める式は以下の通り。

▼ステップ3:n=10の時の分数数列の和を求める。
ステップ2で求めた式に10を代入していくと、分数数列の和を求めることができる。

■分数数列の和の求め方(ループ処理)
前項までで、机上による分数数列の和の算出方法を説明したが、pythonのループ処理を使用してしまえば、第k項の値を算出(前項のステップ1まで)できれば、分数数列の和は計算できる。
■例題
ループ処理を使用して、以下の分数数列の和を求める。
▼問題1
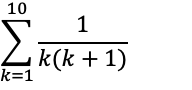
▼問題2
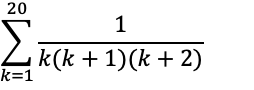
■サンプルコード
# -*- Coding:UTF-8 -*-
# 問題1:Σ 1/(k(k+1)), (n=10, k=1)
# 初期値をセット
n = 10
k = 1
sum1 = 0
# kがnになるまでループ処理
while k <= n:
# 合計を算出
sum1 = sum1 + (1 / (k * (k + 1)))
# インクリメント処理
k += 1
# 少数第2位まで表示
print('問題1:', round(sum1, 2))
# 問題2:Σ 1/(k(k+1)(k+2)), (n=20, k=1)
# 初期値をセット
n = 20
k = 1
sum2 = 0
# kがnになるまでループ処理
while k <= n:
# 合計を算出
sum2 = sum2 + (1 / (k * (k + 1) * (k + 2)))
# インクリメント処理
k += 1
# 少数第2位まで表示
print('問題2:', round(sum2, 2))
■実行結果
問題1: 0.91
問題2: 0.25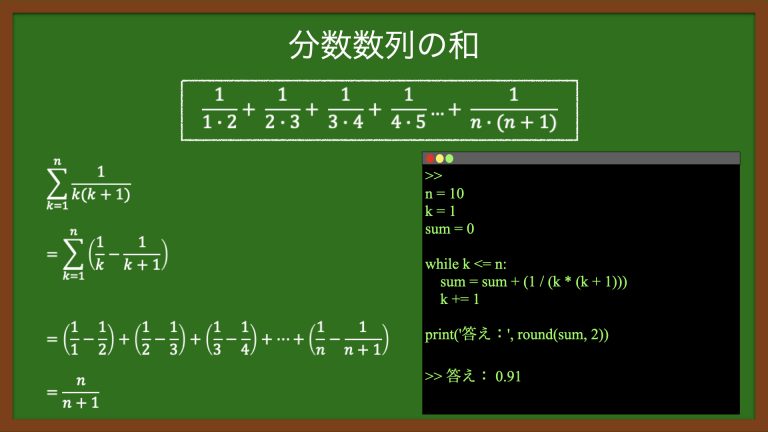

コメント
[…] ソースからの抜粋: … […]
[…] ソースからの抜粋: … […]