■階差数列
任意の数列anにおいて、
bn = an+1 – an (n = 1, 2, 3, …)
と表記できる数列bnを数列anの階差数列という。
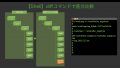
▼イメージ
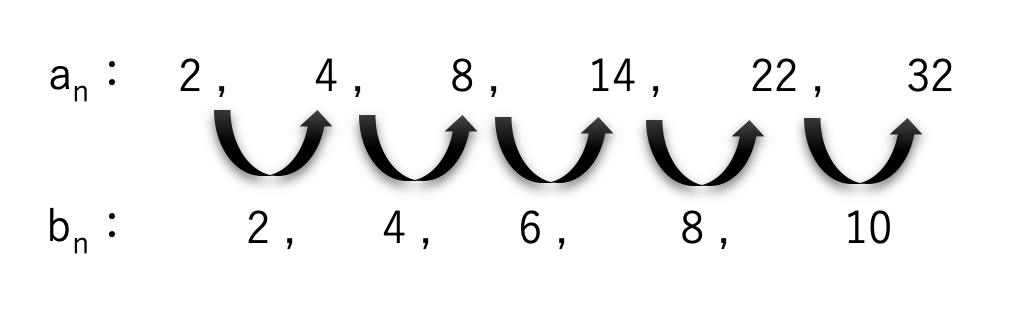
■例題
以下の数列anについて、第10項の値と第10項までの合計値を求める。
an = 2, 4, 8, 14, 22, 32, ・・・
▼階差数列bnを調べる
数列anについて、an+1 – anの値(bn)を調べる。
・サンプルコード
# 初期値をセット
a_array = [2, 4, 8, 14, 22, 32]
b_array = []
i = 0
# 配列(a_array)の要素数-1回分繰り返し
while i < len(a_array) - 1:
# 配列(a_array)の[i+1]番目の要素 - [i]番目の要素の結果を配列(b_array)に格納
b_array.append(a_array[i+1] - a_array[i])
# インクリメント処理
i += 1
print('an:', a_array)
print('bn:', b_array)・実行結果
an: [2, 4, 8, 14, 22, 32]
bn: [2, 4, 6, 8, 10]実行結果より、数列bnは、初項2、公差2の等差数列であることがわかった。
▼数列anの第10項を求める
数列bnが、初項2、公差2の等差数列であることより、数列anの第n項の値は、初項a1と数列bn-1までの和を足し合わせた値であることがわかる。
a1 = a1 + (b0) = 2
a2 = a1 + (b1) = 2 + 2 = 4
a3 = a1 + (b1 + b2) = 2 + (2 + 4) = 6
a4 = a1 + (b1 + b2 + b3) = 2 + (2 + 4 + 6) = 14
↓
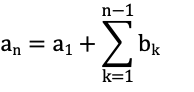
したがって、数列anの第10項は、
a10 = a1 + (b1 + b2 + b3 + … + b9)
より、数列anの初項+数列bnの第9項までの和で求めることができる。
▼等差数列の和の求め方の参照先。
・サンプルコード
# 初期値:項数[N:10項]
a_array = [2, 4, 8, 14, 22, 32]
b_array = [2, 4, 6, 8, 10]
N = 10
# 配列(b_array)関係の値
# 初項(b1)と公差(d)を変数に格納
# 数列(an)の第10項-1(=第9項)
b1 = b_array[0]
d = b_array[1] - b_array[0]
n = N - 1
# a1と配列(b_array)の値を加算する(等差数列の和の公式)
a10 = a_array[0] + ((n * (2 * b1 + (n - 1) * d)) / 2)
print('階差数列の第10項:', a10)
・実行結果
階差数列の第10項: 92.0▼数列anの第10項までの合計値を求める
数列anの第10項を求めることが可能となったため、次は合計値を求める。
求め方は、先ほどの算出方法を第1項から第10項まで繰り返し処理を行い、合算する。
・サンプルコード
# 初期値:項数[N:10項]
a_array = [2, 4, 8, 14, 22, 32]
b_array = [2, 4, 6, 8, 10]
N = 10
# 配列(b_array)関係の値
# 初項(b1)と公差(d)を変数に格納
# 数列(an)の第10項-1(=第9項)
b1 = b_array[0]
d = b_array[1] - b_array[0]
n = N - 1
sum = 0
j = 0
# 10回繰り返し
for j in range(N):
sum = sum + a_array[0] + ((j * (2 * b1 + (j - 1) * d)) / 2)
print('階差数列の第10項までの和:', sum)・実行結果
階差数列の第10項までの和: 350.0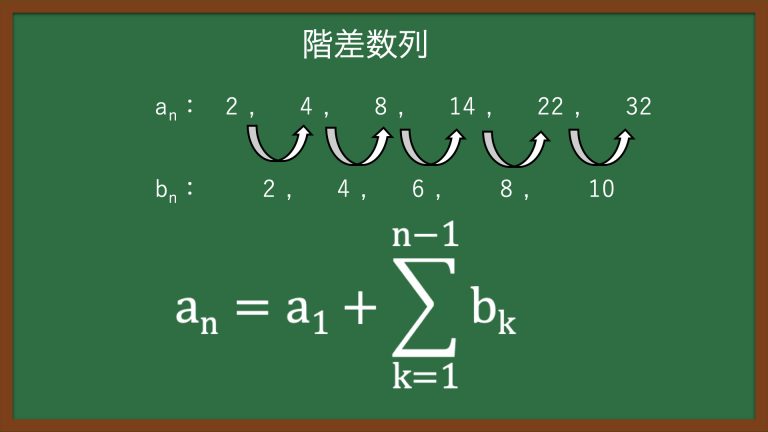

コメント