■無限等比級数
任意の数列anについて、各項の和の式(Sn)を級数と呼ぶ。
an:a1、a2、a3、a4、・・・、an
↓
Sn:a1+a2+a3+a4+・・・+an
このとき、数列Snについて、「n = 1、2、・・・、無限」と続く場合を無限級数と呼ぶ。
S1:a1
S2:a1+a2
S3:a1+a2+a3
:
Sn:a1+a2+a3+a4+・・・+an
:
無限に続く・・・。
また、この無限級数において、数列anが等比数列(初項a、公比r)の場合、無限等比級数と呼ぶ。
an:a、ar、ar2、ar3、・・・、arn-1、・・・
そして、この無限等比級数について、数列Snが一定の値に近づくことを収束と呼び、常に増加・減少し続けることを発散と呼ぶ。
無限等比級数が収束する場合、以下の式で表すことができる。
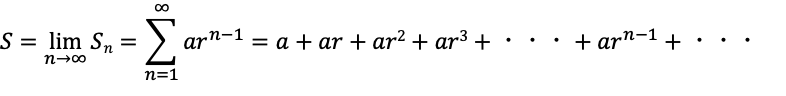
■無限等比級数の収束・発散判定
無限等比級数が収束・発散するかの判定については、下表に示す。
数列anが等比数列(初項a、公比r)の場合
| 区分 | 公比 |
|---|---|
| 収束 | -1 < r < 1 |
| 発散 | r ≦ -1、1 ≦ r |
また、数列anが収束する場合、近似値は以下のように算出できる。
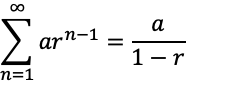
■例題
以下の2つの数列について、等比級数が収束・発散するか判定し、収束する場合は、近似値を求める。
また、数列の和がどのように増加していくかグラフで図示する。
▼問題1

▼問題2
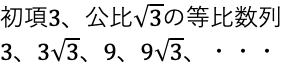
■サンプルコード
# -*- Coding:UTF-8 -*-
import math
import numpy as np
from matplotlib import pyplot as plt
# 無限等比級数を判定・算出する関数
def MugenTohiKyusu(a, r):
# -1 < r < 1 の場合、収束するため、無限等比数を算出する
if r > -1 and r < 1:
result = a / (1 - r)
print('収束')
print('無限等比数:', result)
# r <= -1, r >= 1の場合、発散するため、無限等比級数はない
else:
print('発散')
print('無限等比数:なし')
# 等比数列の和を算出する関数
def SumTohiSuretsu(a: int, r: int, n: int) -> float:
# 合計の初期値をセット
sum = 0
# rについて、1、1より小さい、1より大きいで条件分岐
if r == 1:
# 公式①
sum = a * n
elif r < 1:
# 公式②
sum = (a * (1 - (r ** n))) / (1 - r)
elif r > 1:
# 公式③
sum = (a * ((r ** n) - 1)) / (r - 1)
return sum
# グラフ作成関数
def MakeGraph(a, r):
# 便宜上、第1から10項までの値を0.1間隔で設定
n_min = 1
n_max = 10
n_interval = 0.1
n = np.arange(n_min, n_max, n_interval)
# 等比数列の和を格納する配列
Sn = []
# 第1項、1から2項までの和、1から3項までの和・・・1から10項までの和を
# それぞれ配列に格納していく(便宜上、nは0.1間隔でセット)
for i in range(len(n)):
# i番目までの等比数列の和を配列に格納
Sn.append(SumTohiSuretsu(a, r, n[i]))
# グラフを作成
plt.plot(n, Sn)
# グラフにx軸,y軸(0)を図示
# 補助線(0)を作成 [axhline:水平 axvline:垂直]
plt.axhline(y=0, color="gray")
plt.axvline(x=0, color="gray")
# グラフを表示
plt.show()
# メイン処理
if __name__ == '__main__':
# 問題1
a1 = 1
r1 = 1/2
print('###問題1###')
MugenTohiKyusu(a1, r1)
MakeGraph(a1, r1)
# 問題2
a2 = 3
r2 = math.sqrt(3)
print('###問題2###')
MugenTohiKyusu(a2, r2)
MakeGraph(a2, r2)
■実行結果
▼問題1
###問題1###
収束
無限等比数: 2.0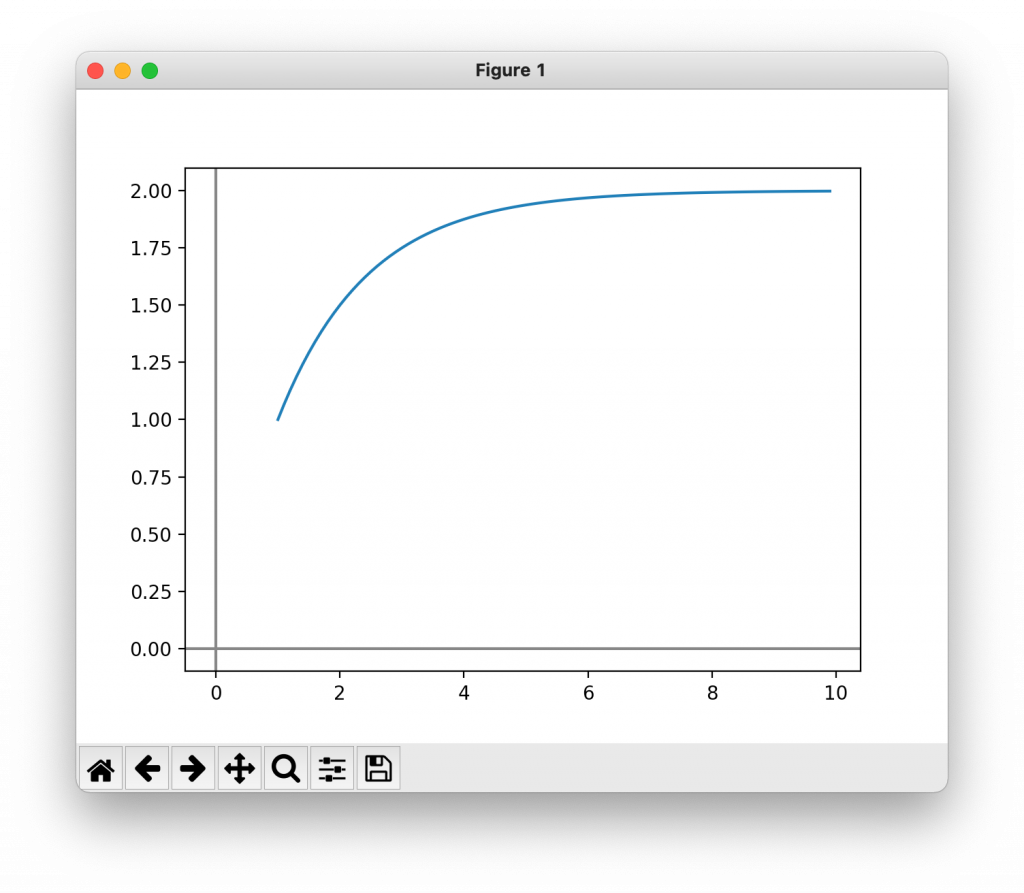
▼問題2
###問題2###
発散
無限等比数:なし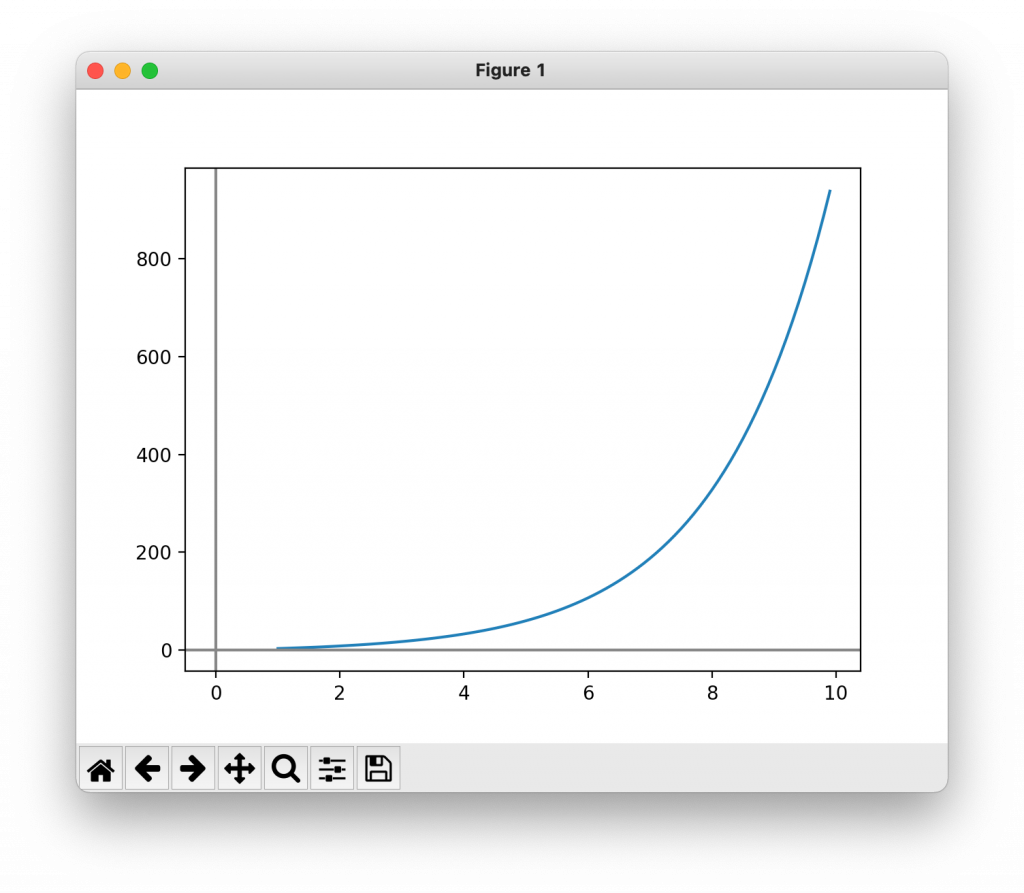


コメント