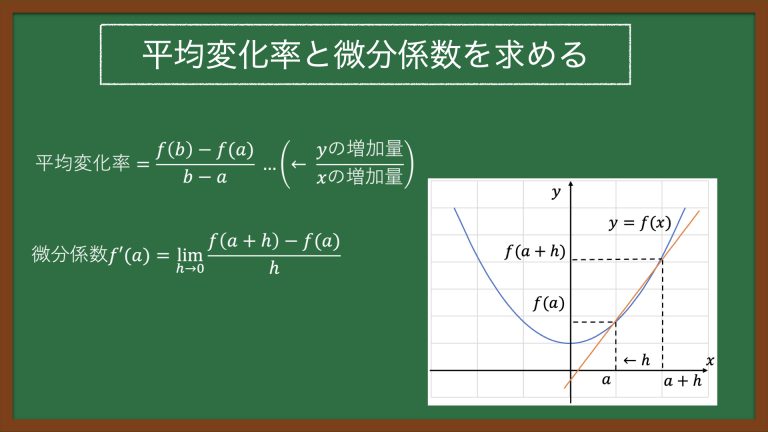
■平均変化率
微分とは、曲線状のある1点における傾きを求めることである。
傾きは、平均変化率(変化の割合)という。
※xが1増加したときのyの増加量(変化量)
関数 y = f(x) において、xがaからbまで変化した時、平均変化率は以下の式で求める。
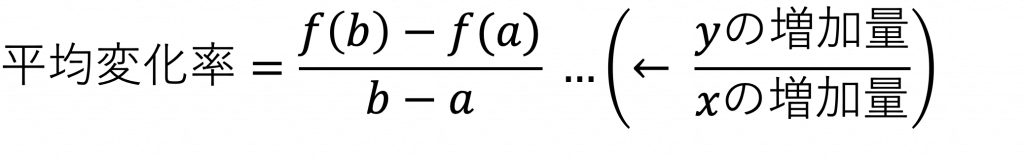
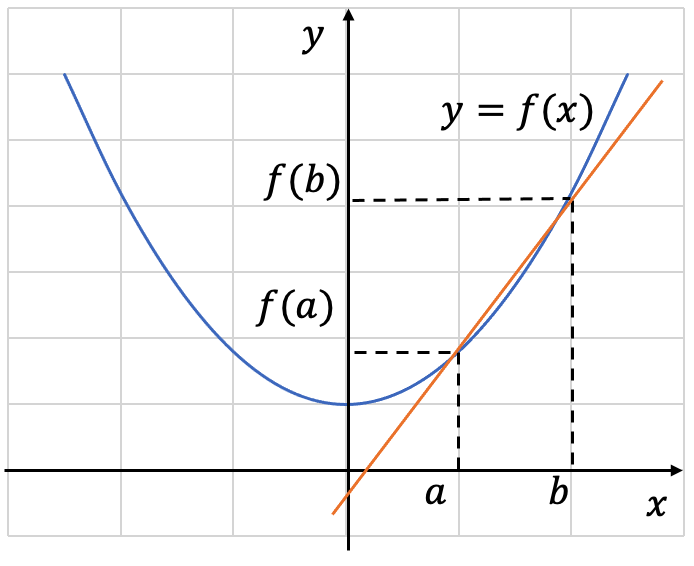
■微分係数
関数 y = f(x) において、xがaからbまで変化した時、平均変化率(変化の割合)を求める時、bの値を限りなくaに近づげていく(xの増加量を限りなく小さくしていく)と、曲線上にある1点の傾きを求めることができる。
x = a における平均変化率を求めることを微分係数を求めるといい、f'(a)と表す。
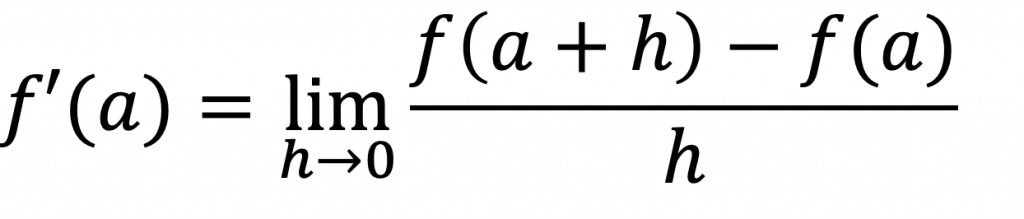
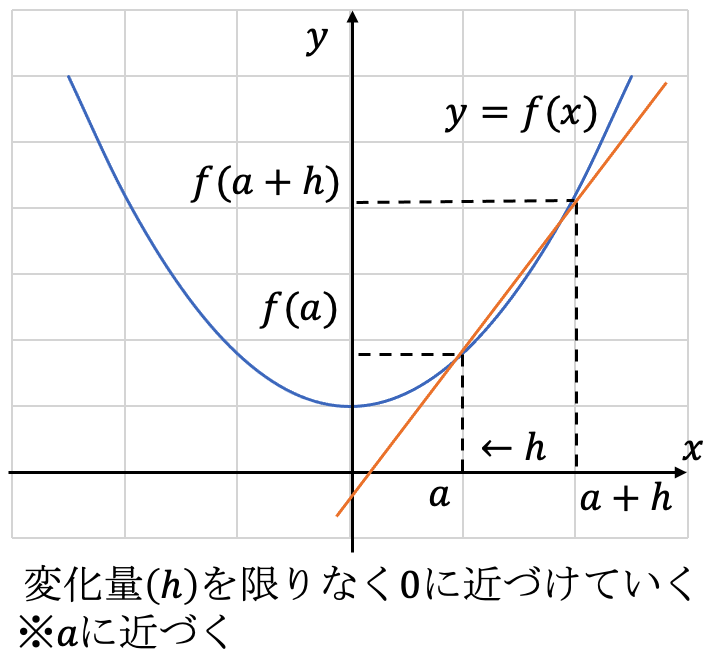
f'(a)とは、点(a, f(a))における接戦の傾きである。
■例題
関数f(x)=x2+xについて、以下の3問をPythonを使用して解く。
問題1
xが1から2まで変化する時の平均変化率を求める。
問題2
x = 1における微分係数f'(1)を求める。
問題3
f(x)とA(1,f(1))を通るf(x)の接線をグラフに図示
■サンプルコード
# -*- Coding:UTF-8 -*-
import sympy
import numpy as np
from matplotlib import pyplot as plt
# f(x)=x**2 + xの値を求める関数
def f(x):
y = x**2 + x
return y
# 平均変化率を求める関数
def henkaritsu(a, b):
# 平均変化率を求める
result = (f(b) - f(a)) / (b - a)
# 計算結果を返す
return result
# 微分係数を求める関数
def f_(a):
# 文字列をセット
h = sympy.Symbol('h')
# 微分係数を求める
result = sympy.limit((f(a+h)-f(a))/h, h, 0)
# 計算結果を返す
return result
# グラフ作成関数
def MakeGraph(sessen_katamuki, sessen_seppen):
# 便宜上、-5から5までの値を0.1間隔で設定
x_min = -5
x_max = 5
x_interval = 0.1
x = np.arange(x_min, x_max, x_interval)
# 関数f(x)を格納する配列
y1 = []
# 接線のyの値を格納する配列
y2 = []
# それぞれ配列に格納していく(便宜上、nは0.1間隔でセット)
for i in range(len(x)):
y1.append(f(x[i]))
y2.append((sessen_katamuki * x[i]) + sessen_seppen)
# 関数f(x)のグラフを作成
plt.plot(x, y1)
# 接線のグラフを作成
plt.plot(x, y2)
# グラフにx軸,y軸(0)を図示
# 補助線(0)を作成 [axhline:水平 axvline:垂直]
plt.axhline(y=0, color="gray")
plt.axvline(x=0, color="gray")
# グラフを表示
plt.show()
# メイン処理
if __name__ == '__main__':
# 問題1:xが1から2まで変化する時の平均変化率を求める
ans1 = henkaritsu(1, 2)
print('問題1:', ans1)
# 問題2:x=1における微分係数f'(1)を求める
ans2 = f_(1)
print('問題2:', ans2)
# 問題3:f(x)とA(1,f(1))を通るf(x)の接線をグラフに図示
# 接線の傾き(a)は問題2の値
sessen_a = ans2
# 接線の切片(b)を求める(y = ax + b)
sessen_b = f(1) - sessen_a * 1
# グラフの作成
print('問題3')
print('接線:y = ', sessen_a, 'x + (', sessen_b, ')')
MakeGraph(sessen_a, sessen_b)
■実行結果
問題1: 4.0
問題2: 3
問題3
接線:y = 3 x + ( -1 )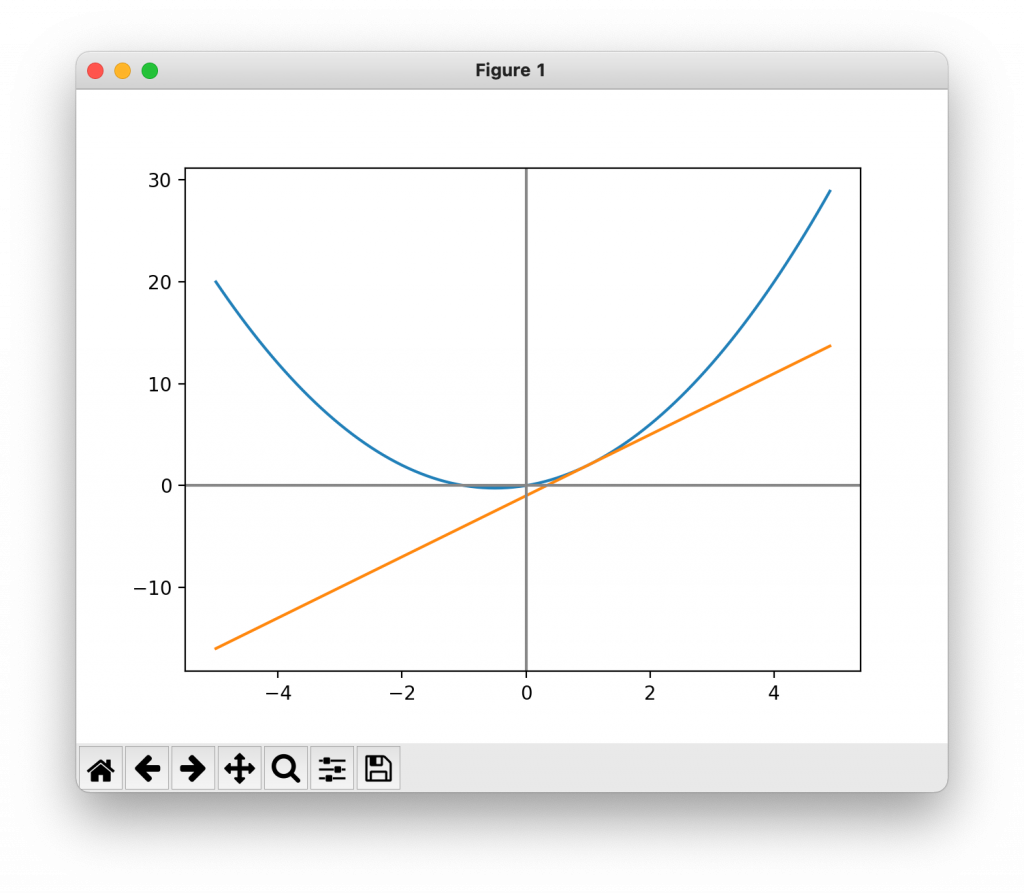


コメント