■場合の数
場合の数とは、ある事象について、起こりうるすべてのパターン数を表す。
例えば、サイコロの出る目について、すべてのパターンは、以下の6通りである。
「1」、「2」、「3」、「4」、「5」、「6」
▼積の法則
同時に起こりうる「A」、「B」の2つの事象について、
「A」の起こりうる場合の数を「a」、
「B」の起こりうる場合の数を「b」とし、
「A」と「B」がともに起こりうる場合の数は、「a × b」通りである。
■例題
以下図において、地点「A」、「B」、「C」を通る行き方は何通りあるか、pythonで実装する。
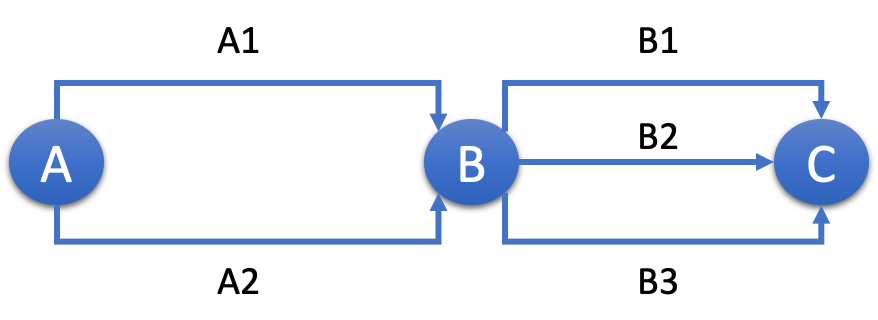
▼机上計算
図の通り、地点「A」から「B」、地点「B」から「C」は、同時に起こりうる事象であるため、「積の法則」を使用する。
地点「A」から「B」は、「A1」および「A2」の2通り、
地点「B」から「C」は、「B1」、「B2」、「B3」の3通りであるため、
2 × 3 = 6(通り)である。
■Pythonによる実装
▼フローチャート
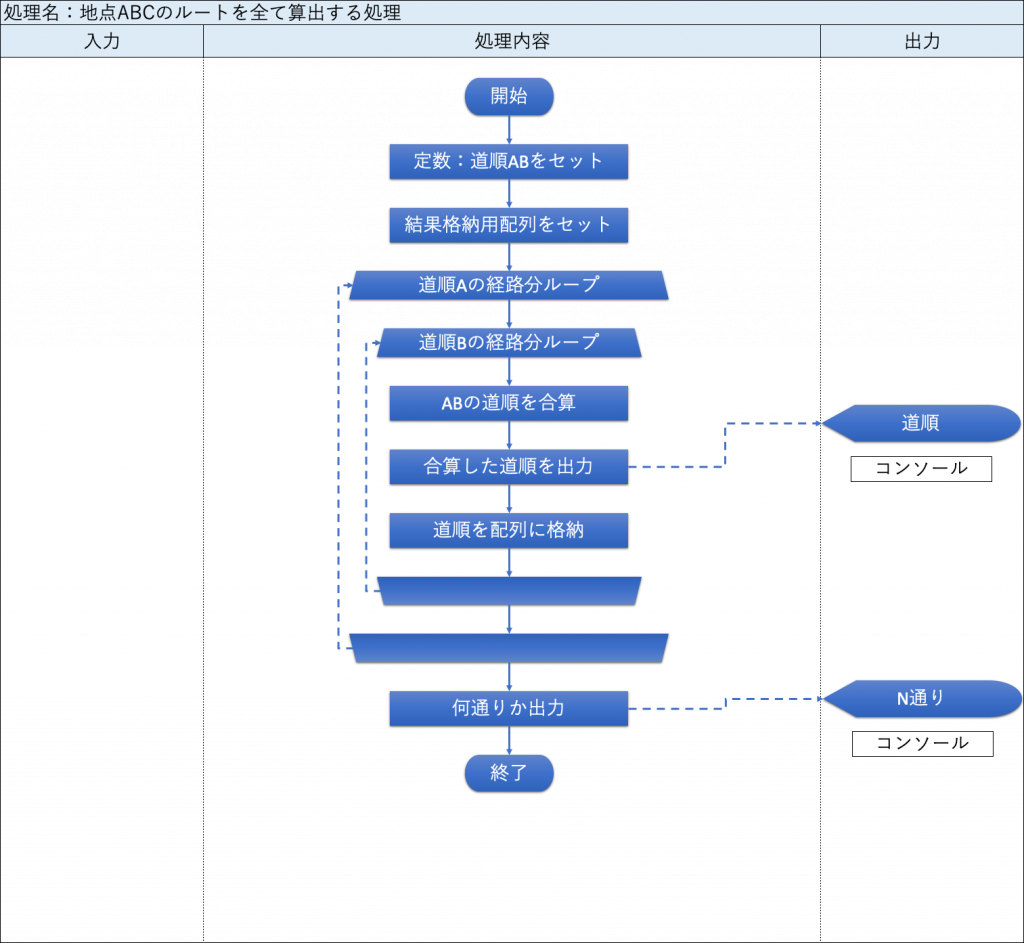
▼プログラム仕様
| 入力 | 処理内容 | 出力 |
|---|---|---|
| – | 定数:道順をセットする。 道順A=「A1、A2」 道順B=「B1、B2、B3」 | – |
| – | 結果格納用配列をセットする。 初期値:[] | – |
| – | ■ループ処理:道順A分繰り返し |■ループ処理:道順B分繰り返し ||道順ABを合算する。(例:A1B1) ||道順を表示する。 ||結果格納配列に合算値を格納する。 |■ ■ | 【コンソール】 道順 |
| – | 答え:結果格納配列の要素数を出力する。 | 【コンソール】 N通り ※Nは任意の数 |
▼サンプルコード
# 地点ABCのルートを全て算出する処理
def cal_cases_A_B_C():
# 定数を設定
LIST_A = ['A1', 'A2']
LIST_B = ['B1', 'B2', 'B3']
# 結果格納用配列
list_result = []
# Aのルート分ループ
for i in range(len(LIST_A)):
# Bのルート分ループ
for j in range(len(LIST_B)):
# ABの道順を合算
case_abc = LIST_A[i]+LIST_B[j]
# 道順を表示
print(case_abc)
# 配列に格納
list_result.append(case_abc)
# 答え:配列の要素数を出力
print('答え:', len(list_result), '通り')
# メイン処理
if __name__ == '__main__':
cal_cases_A_B_C()
▼実行結果
A1B1
A1B2
A1B3
A2B1
A2B2
A2B3
答え: 6 通り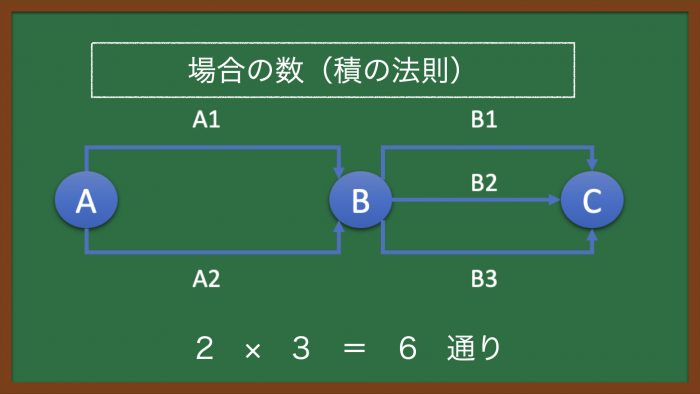
コメント