■概要
場合の数のうち、重複順列について、
机上計算とPythonを使用した計算処理の2種類の解答方法を示す。
なお、今回はじゃんけんの出す手の場合の数を求める。

■重複順列
異なるn個のものから、同じものについて、重複を許してr個とる順列を「重複順列」という。
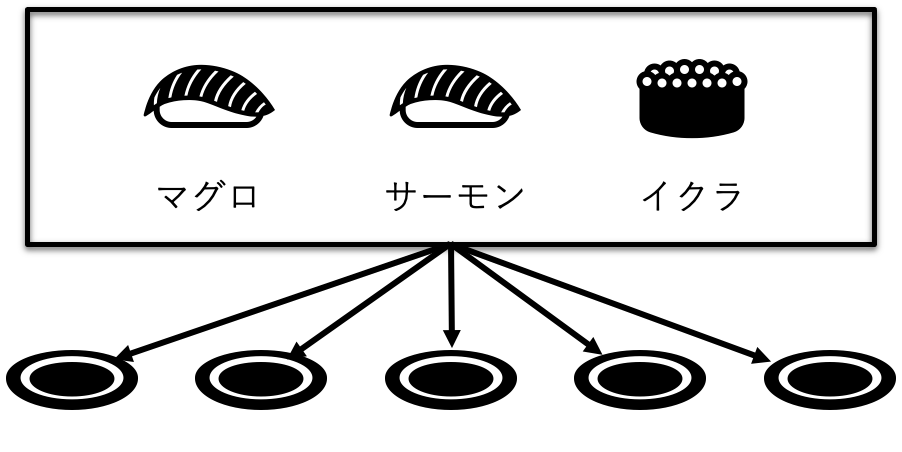
下図のように、「マグロ」、「サーモン」、「イクラ」の寿司のうち、
好きなものを5皿選ぶ場合の数は、
・1皿目:「マグロ」、「サーモン」、「イクラ」の3通り
・2皿目:「マグロ」、「サーモン」、「イクラ」の3通り
・3皿目:「マグロ」、「サーモン」、「イクラ」から3通り
・4皿目:「マグロ」、「サーモン」、「イクラ」から3通り
・5皿目:「マグロ」、「サーモン」、「イクラ」から3通り
となるので、求める場合の数は、以下の通り求める。
3 × 3 × 3 × 3 × 3
= 35
= 243通り
▼重複順列の公式
異なるn個のものから、同じものについて、重複を許してr個とる順列は以下の通り計算する。
n × n × n × n × n × ・・・ × n
= nr
= nΠr(パイのn、r)
■例題
▼問1
Aさん、Bさん、Cさんの3人でじゃんけんをしたとき、3人の出す手は何通りあるか。
▼問2
Aさん、Bさん、Cさん、Dさんの4人でじゃんけんをしたとき、4人の出す手は何通りあるか。
■机上計算
▼問1
3人でじゃんけんをした時、3人とも「グー」・「チョキ」・「パー」の3つの手を出すことができる。
したがって、3人の出す手の場合の数は、以下の通りとなる。
3Π3
= 33
= 3 × 3 × 3
= 27 通り
▼問2
4人でじゃんけんをした時、4人とも「グー」・「チョキ」・「パー」の3つの手を出すことができる。
したがって、4人の出す手の場合の数は、以下の通りとなる。
3Π4
= 34
= 3 × 3 × 3 × 3
= 81 通り
■Pythonによる実装
▼フローチャート
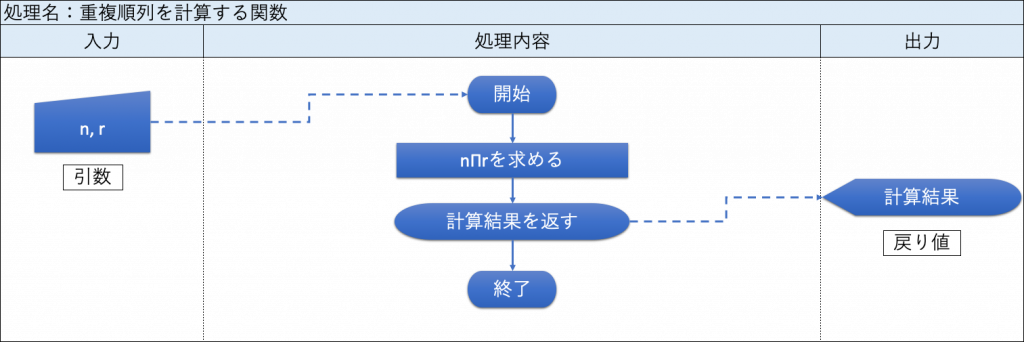
重複順列を計算する関数について、フローチャートを下図に示す。
▼プログラム仕様
<処理名:重複順列を計算する関数>
・引数と戻り値
| 項目 | 値 | 内容 |
|---|---|---|
| 第1引数 | n | nΠrのうち、「n」 |
| 第2引数 | r | nΠrのうち、「r」 |
| 戻り値 | 計算結果 | 重複順列の計算結果 |
・処理概要
| 入力 | 処理内容 | 出力 |
|---|---|---|
| – | 重複順列の計算を行う。 nΠr = nr | – |
| – | 重複順列の計算結果を戻り値として返す。 | – |
▼サンプルコード
# 重複順列を計算する関数
def cal_duplicate(n: int, r: int) -> int:
# 重複順列を求める(nΠr)
ans = n ** r
return ans
# メイン処理
if __name__ == '__main__':
# 問1:3人でじゃんけんする場合(3Π3)
print('3人:', cal_duplicate(3, 3), '通り')
# 問2:4人でじゃんけんする場合(3Π4)
print('4人:', cal_duplicate(3, 4), '通り')
▼実行結果
3人: 27 通り
4人: 81 通り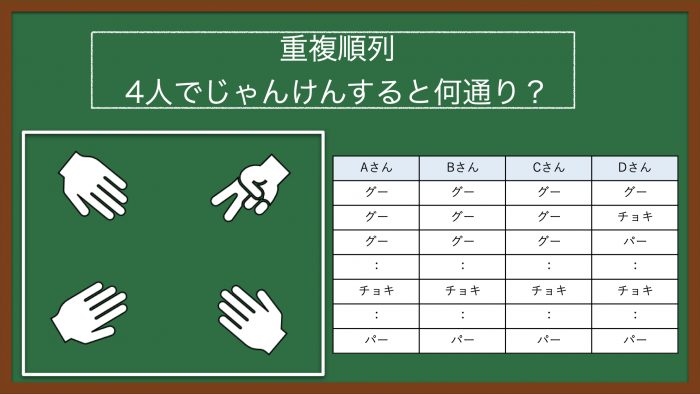


コメント