【Python】 2次関数　軸方程式と任意の2点A, Bから2次関数を求めてグラフに図示

■2次関数

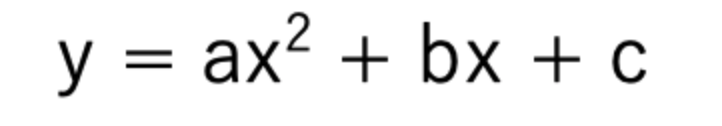
a > 0 の時、グラフは下に凸（とつ）

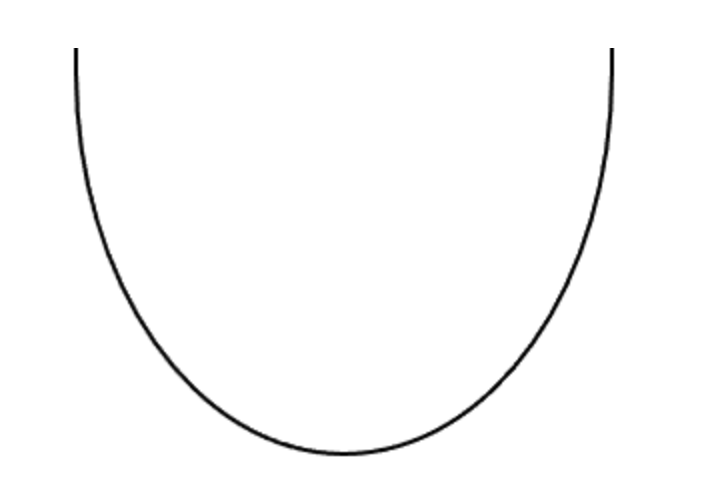
a < 0 の時、グラフは上に凸（とつ）

■軸方程式を算出

2次関数について平方完成をすると・・・

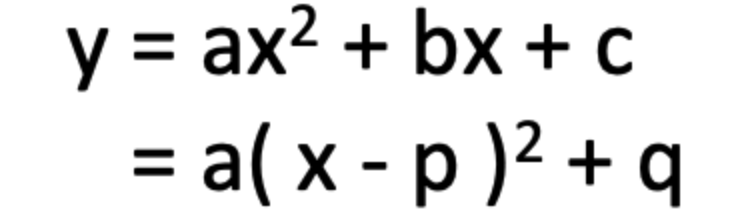
このとき
・頂点座標（p, q）
・軸の方程式： x = p
が成り立つ。

■軸方程式と任意の2点A, Bから2次関数を算出

軸方程式：x = p
2点：A(x1, y1), B(x2, y2)
の場合・・・

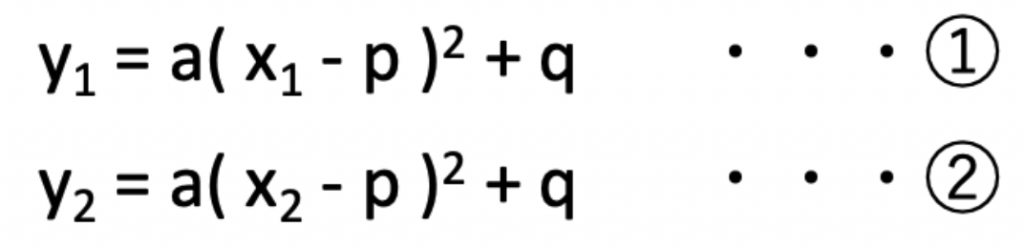
①、②より、aとqの連立方程式を解く

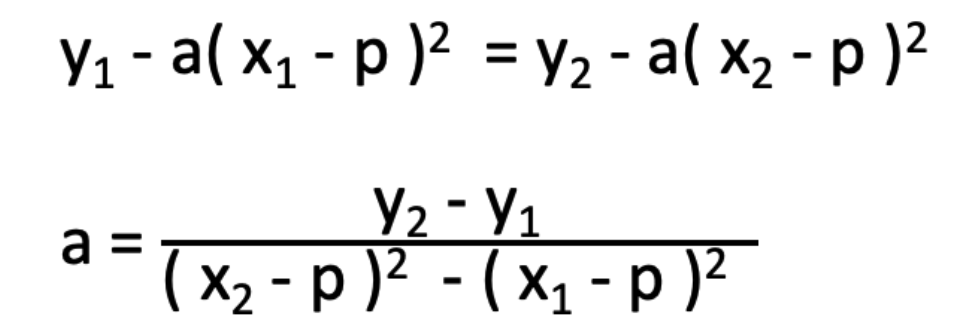
求めたaを①に代入してqを算出

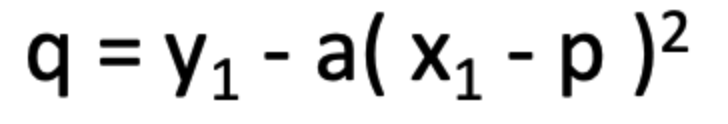
■例題

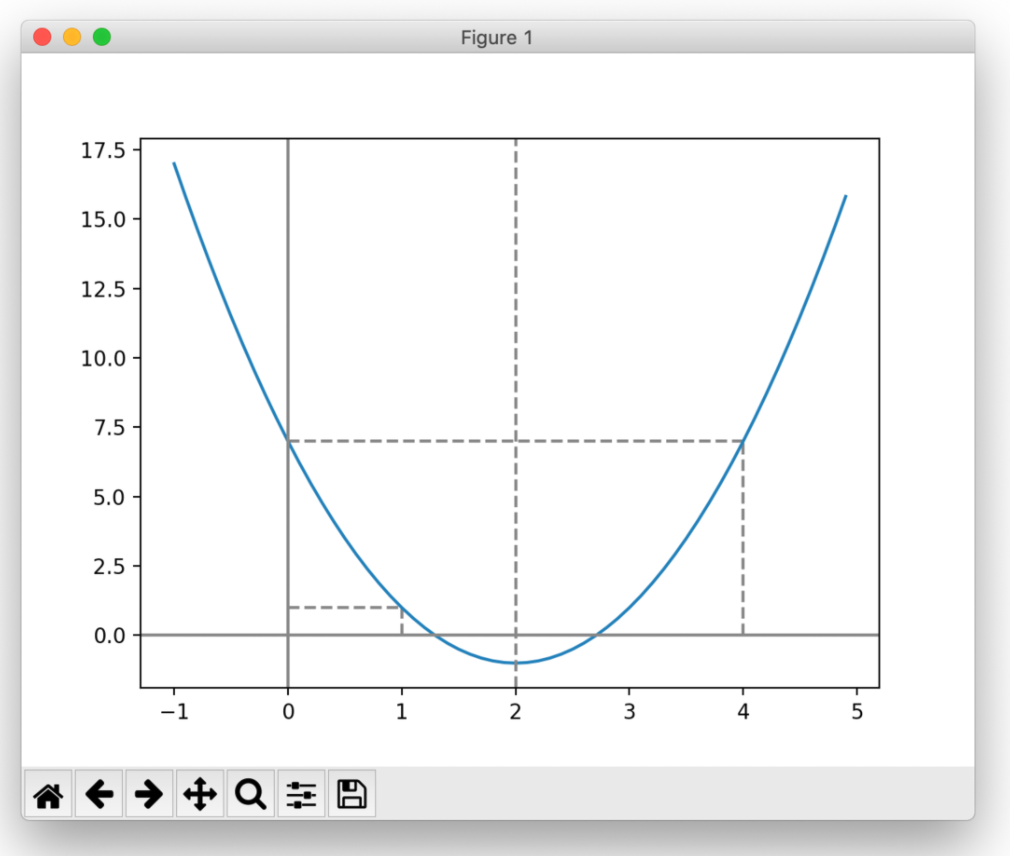
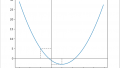
軸方程式：x = 2、2点(1, 1) (4, 7)を通る2次関数を求め、グラフに図示

■サンプルコード

# -*- Coding: UTF-8 -*-
import numpy as np
from matplotlib import pyplot as plt

# 2次関数の軸の方程式と任意の2点A, Bから2次関数を決定する関数
# 平方完成の y = a(x - p)**2 + q を使用
# 引数     ： 軸の方程式 x = p の [p]
#            任意の2点A(x1, y1)、B(x2, y2)
# 戻り値   ：y = a(x - p)**2 + q の [a, q]
def DecisionQuadraticFunc(p:int, x1:int, y1:int, x2:int, y2:int) -> list:
    # 戻り値用の配列をセット
    result_data = []

    # aの値を算出
    a = (y2 -y1) / (((x2 - p) ** 2 ) - ((x1 - p) ** 2))

    # 配列にaの値を追加
    result_data.append(a)

    # qの値を算出
    q = y1 - ( a * ((x1 - p) ** 2))

    # 配列にqの値を追加
    result_data.append(q)

    return result_data

# グラフを作成する関数
# 引数   ： y = a(x - p)**2 + q の[a]・頂点座標（p, q）・点P(x1, y1)
def MakeGraph(a:int, p:int, q:int, x1:int, y1:int, x2:int, y2:int):

    ########## 2次関数をグラフに図示 ##########
    # 2次関数のxを便宜上、0.1間隔で　-1 < x < 5 の範囲を指定
    xmin = -1
    xmax = 5
    xinterval = 0.1
    x = np.arange(xmin, xmax, xinterval)

    # yを算出
    y = a * (x - p) ** 2 + q

    # グラフを作成
    plt.plot(x,y)
    ########################################

    ########## グラフに軸方程式 x = pを図示 ##########
    plt.axvline(x = p, color = "gray", linestyle='dashed')
    ###################################################

    ########## グラフにx軸,y軸から点Aまでを点線で図示 ##########
    # 補助線を点線で作成　[hlines：水平　vlines:垂直]
    plt.hlines([y1], 0, x1, "gray", linestyles='dashed')
    plt.vlines([x1], 0, y1, "gray", linestyles='dashed')
    #######################################################

    ########## グラフにx軸,y軸から点Bまでを点線で図示 ##########
    # 補助線を点線で作成　[hlines：水平　vlines:垂直]
    plt.hlines([y2], 0, x2, "gray", linestyles='dashed')
    plt.vlines([x2], 0, y2, "gray", linestyles='dashed')
    #######################################################

    ########## グラフにx軸,y軸（0）を図示 ##########
    # 補助線（0）を作成　[axhline：水平　axvline:垂直]
    plt.axhline(y = 0, color = "gray")
    plt.axvline(x = 0, color = "gray")
    ############################################

    # グラフを表示
    plt.show()


# メイン処理
if __name__ == '__main__':
    # 軸方程式 x=2と2点A(1,1)、B(4,7)を通る2次関数を求める
    p = 2
    x1 = 1
    y1 = 1
    x2 = 4
    y2 = 7


    # 軸方程式と任意の2点A, Bから2次関数を決定する
    result_data = DecisionQuadraticFunc(p, x1, y1, x2, y2)

    a = result_data[0]
    q = result_data[1]

    print('二次関数：y = ' + str(a) + '( x - ( ' + str(p) + ' )) ** 2 + ( ' + str(q) + ' )')

    # グラフの作成
    MakeGraph(a, p, q, x1, y1, x2, y2)

■実行結果

二次関数：y = 2.0( x – ( 2 )) ** 2 + ( -1.0 )