■余弦定理
余弦定理:
余弦(cos)を使用して、三角形の3辺と1つの内角の関係を表す。
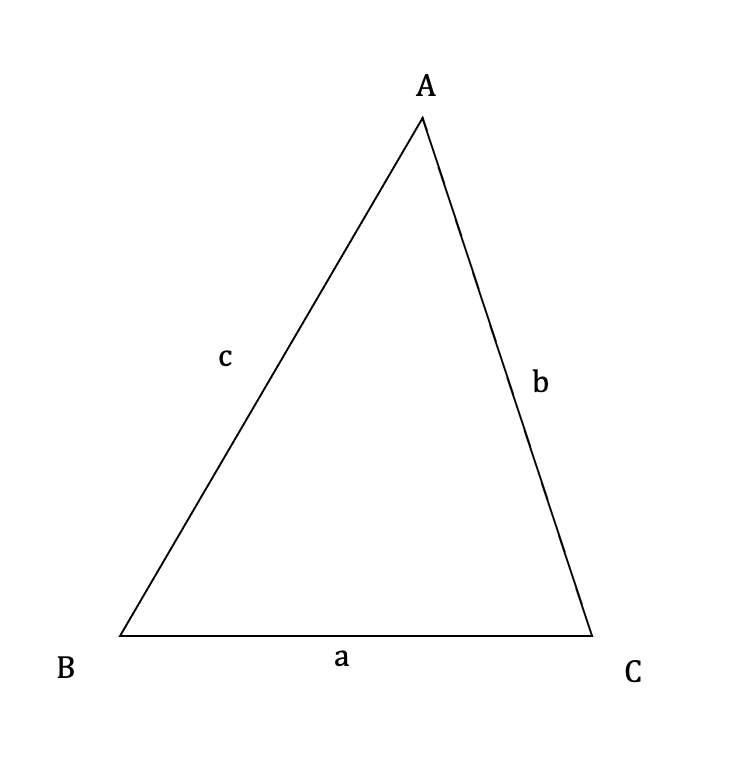
上記の三角形ABCにおける、辺a、b、cおよび角度A、B、Cについて、
以下の公式が成り立つ。
a2 = b2 + c2 – 2bccosA
b2 = c2 + a2 – 2cacosB
c2 = a2 + b2 – 2abcosC
■例題
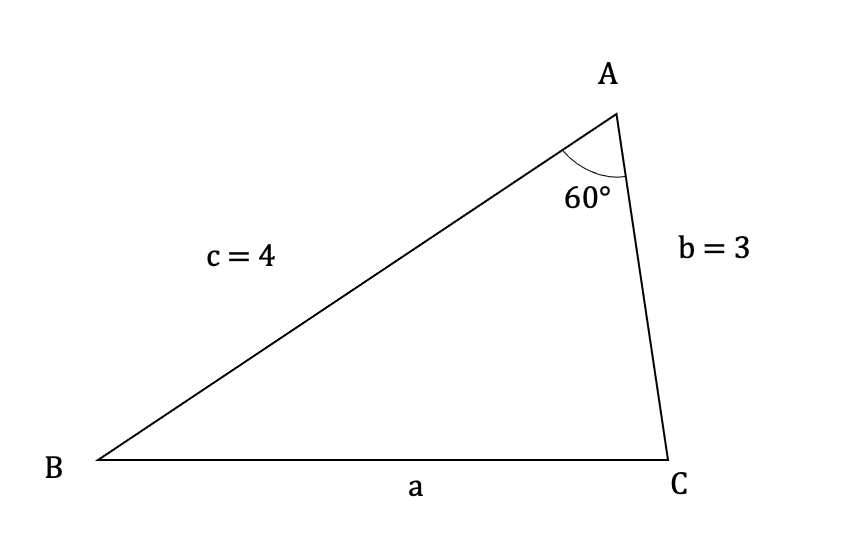
三角形ABCにおいて、b = 3、c = 4、A = 60°のとき、辺aの長さ、角度B、角度Cを求める。
■サンプルコード
# -*- Coding:UTF-8 -*-
import math
# 初期値の設定
b = 3
c = 4
A = 60
# 角度をラジアンに変換
radianA = math.radians(A)
# 余弦定理、a**2 = b**2 + c**2 - 2bccosAよりa2乗を求める
a_2 = b**2 + c**2 - (2 * b * c * math.cos(radianA))
# a > 0よりa_2(a**2)の値は正のみ
a = math.sqrt(a_2)
# 余弦定理、b**2 = c**2 + a**2 - 2cacosBよりcosBを求める
cosB = (c**2 + a**2 - b**2) / (2 * c * a)
# cosBの値からラジアンに変換(逆余弦関数)
radianB = math.acos(cosB)
# ラジアンから角度に変換
B = math.degrees(radianB)
# 余弦定理、c2 = a2 + b2 - 2abcosCよりcosCを求める
cosC = (a**2 + b**2 - c**2) / (2 * a * b)
# cosBの値からラジアンに変換(逆余弦関数)
radianC = math.acos(cosC)
# ラジアンから角度に変換
C = math.degrees(radianC)
print('辺a = ', round(a, 1))
print('角度B = ', round(B, 1))
print('角度C = ', round(C, 1))
★逆余弦関数とは、三角関数(余弦関数)の逆関数であり、アークコサインという。
pythonのmath.acos(コサインの値)メソッドを使用することで、コサインの値からラジアンを算出することができる。
■実行結果
辺a = 3.6
角度B = 46.1
角度C = 73.9

コメント
[…] 1: 余弦定理とは何か?図解でわかるその使い道と公式の証明 2: 【Python】余弦定理を使って問題を解く – え〜のう […]