■等差数列
等差数列とは、隣り合う2項の差が一定の数列である。
(例)
1、4、7、10、13、16、19 ・・・・・・①
上記(例:①の数列)について、ひとつひとつの値を「項」と呼び、
最初の項を「初項」、隣り合う2項の差を「公差」と呼ぶ。
したがって、①の数列は「初項1、公差3の等差数列」である。
■等差数列の公式
等差数列:a1、a2、a3、a4、a5、a6、a7・・・an・・・・・・②
上記②の等差数列について、初項をa、公差をdとするとき、第N番目の項an(一般項)は
an = a + (n – 1)d
と表すことができる。
■例題
等差数列の公式「a + (n – 1)d」を使用し、
初項が3、公差4の等差数列について、1から10番目までの項を求める。
■サンプルコード
# -*- Coding:UTF-8 -*-
# 等差数列の関数
# 引数
# a:初項
# d:公差
# n:N番目まで繰り返す用の値
def ArithmeticalProgression(a:int, d:int, n:int) -> list:
# ループ用初期値(ループカウンタ)
i = 1
# 戻り値用配列をセット
ans = []
# N番目の値が格納されるまで処理を繰り返す
while len(ans) < n:
# 等差数列の公式(a + (i - 1)d)の結果を配列に格納
ans.append(a + (i - 1) * d)
# ループカウンタをインクリメントする
i = i + 1
# 戻り値として、配列を返す
return ans
# メイン処理
if __name__ == '__main__':
# 初項:3、公差:4、10番目まで値を取得
a = 3
d = 4
n = 10
# 等差数列関数を呼び出し結果を格納
result = ArithmeticalProgression(a, d, n)
# 結果を表示する
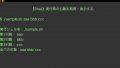
print(result)■実行結果
[3, 7, 11, 15, 19, 23, 27, 31, 35, 39]■参考:range()を使用する場合
range()関数を使用して例題を解く。
▼コード
a = 3
d = 4
ans_range = [i for i in range(a, 40, d)]
print(ans_range)▼実行結果
[3, 7, 11, 15, 19, 23, 27, 31, 35, 39]▼補足説明
range()関数は
range(開始, 終了, 間隔)を設定することができる。
開始値から間隔値を足していき、終了値は指定した値(項)未満までとなることに注意
※ここでは、便宜上、終了値を40としている。
■参考:numpyのarangeを使用する場合
numpyのarangeを使用しても例題を解くことが可能
▼コード
import numpy as np
a = 3
d = 4
ans_numpy = np.arange(a, 40, d)
print(ans_numpy)▼実行結果
[ 3 7 11 15 19 23 27 31 35 39]▼補足説明
numpyのarangeもrange()関数と同様に
arange(開始, 終了, 間隔)を設定することができる。
開始値から間隔値を足していき、終了値は指定した値(項)未満までとなることに注意
※ここでは、便宜上、終了値を40としている。


コメント
[…] 【Python】等差数列:1からN番目までの値(項)を表示する■等差数列等差数列とは、隣り合う2項の差が一定の数列である。(例)1、4、7、10、13、16、19 ・・・・・・①上記(例:①の数 […]
[…] 【Python】等差数列:1からN番目までの値(項)を表示する■等差数列等差数列とは、隣り合う2項の差が一定の数列である。(例)1、4、7、10、13、16、19 ・・・・・・①上記(例:①の数 […]