【Python】等差数列の和の公式を使って問題を解く / え〜のう

■等差数列の和の公式
■例題
■サンプルコード
■実行結果

■等差数列の和の公式

初項：a , 公差：d ,項数：n ,末項：l のとき、等差数列の和Snは、以下のように求めることができる。

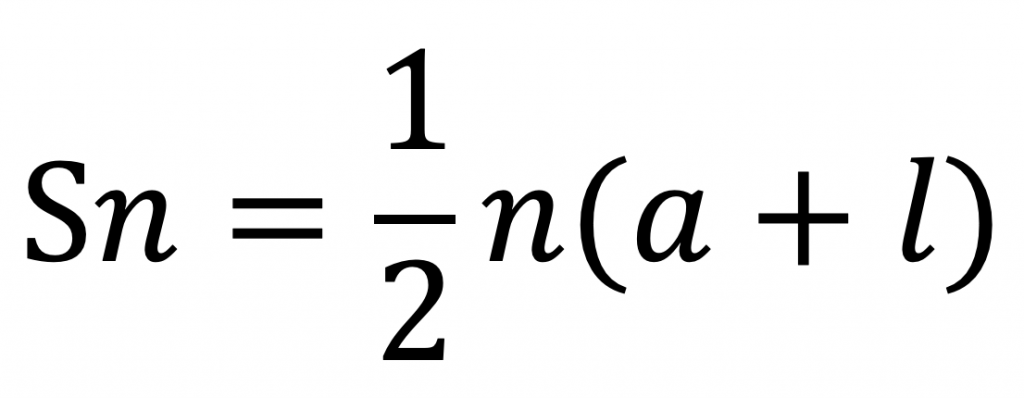
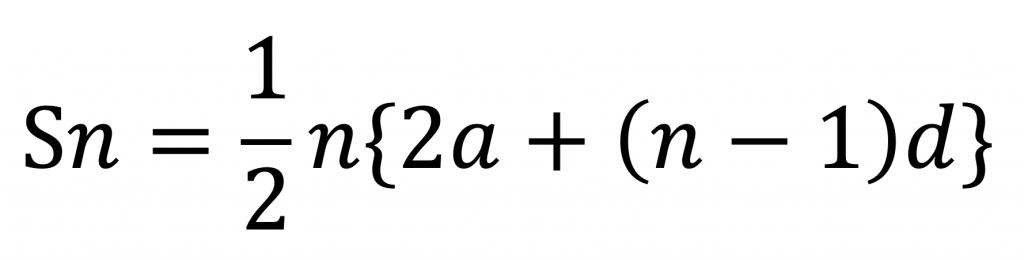
※等差数列についての参照先。

■等差数列等差数列とは、隣り合う2項の差が一定の数列である。（例）1、4、7、10、13、16、19 ・・・・・・①上記（例：①の数列）について、ひとつひとつの値を「項」と呼び、最初の項を「初項」、隣り合う2項の差を「公差」と呼ぶ。したがっ...

■例題

（1）初項2、公差3、項数17の等差数列の和を求める。

（2）初項10、末項-32、項数15の等差数列の和を求める。

■サンプルコード

# -*- Coding:UTF-8 -*-

# 等差数列の和を算出する関数(初項・項数・公差ver)
# 引数
#   a：初項(int)
#   d：公差(int)
#   n：項数(int)
# 戻り値
#   等差数列の和(float)
def Sum_a_d_n(a:int, d:int, n:int) -> float:

    # 等差数列の和の公式
    sum = (n * (2 * a + (n - 1) * d)) / 2

    # 戻り値として、等差数列の和を返す
    return sum


# 等差数列の和を算出する関数(初項・項数・末項ver)
# 引数
#   a：初項(int)
#   l：末項(int)
#   n：項数(int)
# 戻り値
#   等差数列の和(float)
def Sum_a_l_n(a:int, l:int, n:int) -> float:

    # 等差数列の和の公式
    sum = (n * (a + l)) / 2

    # 戻り値として、等差数列の和を返す
    return sum

# メイン処理
if __name__ == '__main__':
    # (1)初項：2、公差：3、項数：17の等差数列の和
    a = 2
    d = 3
    n = 17

    # 等差数列関数を呼び出し結果を格納
    result = Sum_a_d_n(a, d, n)

    # 結果を表示する
    print(result)

    # (2)初項：10、末項：-32、項数：15の等差数列の和
    a = 10
    l = -32
    n = 15

    # 等差数列関数を呼び出し結果を格納
    result = Sum_a_l_n(a, l, n)

    # 結果を表示する
    print(result)