■行列
数や記号や式などを縦と横に矩形状に配列したものである。
(例)
・二次元行列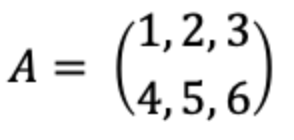
・三次元行列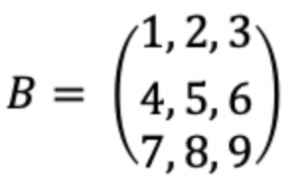
■行列の和と差
行列の和と差は以下のように求める。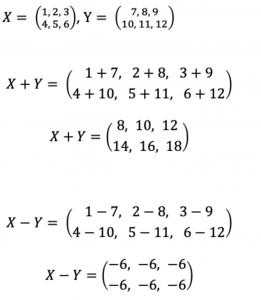
■例題
以下の多次元行列について、それぞれ和と差を求める。
★行列の計算はNumpyの配列を使用することで計算することができる。
▼問題1(2次元行列)
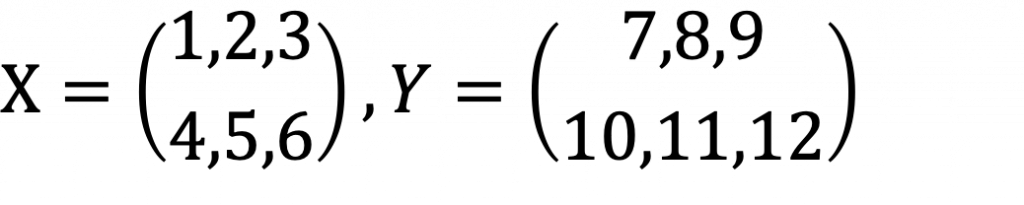
▼問題2(3次元行列)
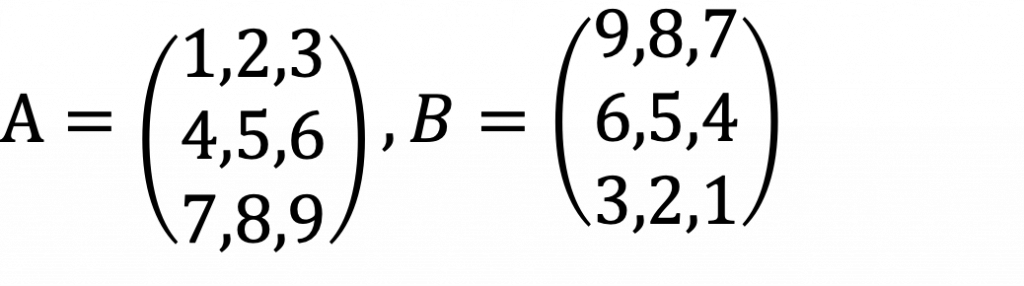
■サンプルコード
▼問題1
# -*- Coding: UTF-8 -*-
import numpy as np
# 多次元配列を変数に格納
X = np.array([[1, 2, 3], [4, 5, 6]])
Y = np.array([[7, 8, 9], [10, 11, 12]])
# 多次元配列の和と差を算出
sum_val = X + Y
sum_def = X - Y
print("多次元配列の和:\n" + str(sum_val))
print("多次元配列の差:\n" + str(sum_def))
▼問題2
# -*- Coding: UTF-8 -*-
import numpy as np
# 多次元配列を変数に格納
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
B = np.array([[9, 8, 7], [6, 5, 4], [3, 2, 1]])
# 多次元配列の和と差を算出
sum_val = A + B
sum_def = A - B
print("多次元配列の和:\n" + str(sum_val))
print("多次元配列の差:\n" + str(sum_def))■実行結果
▼問題1
多次元配列の和:
[[ 8 10 12]
[14 16 18]]
多次元配列の差:
[[-6 -6 -6]
[-6 -6 -6]]▼問題2
多次元配列の和:
[[10 10 10]
[10 10 10]
[10 10 10]]
多次元配列の差:
[[-8 -6 -4]
[-2 0 2]
[ 4 6 8]]■参考:リスト型の配列で和と差を求める
Numpyを使用せず、リスト型にて+を使用すると、計算を行うのではなく、配列が連結される。
※「ー」については、エラーとなる。
▼サンプルコード
# -*- Coding: UTF-8 -*-
# 多次元配列を変数に格納
A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
B = [[9, 8, 7], [6, 5, 4], [3, 2, 1]]
# 多次元配列の和と差を算出
sum_val = A + B
print("多次元配列の和:\n" + str(sum_val))
sum_def = A - B
print("多次元配列の差:\n" + str(sum_def))▼実行結果
多次元配列の和:
[[1, 2, 3], [4, 5, 6], [7, 8, 9], [9, 8, 7], [6, 5, 4], [3, 2, 1]]
unsupported operand type(s) for -: 'list' and 'list'赤字部分については、配列同士を「ー」した場合に発生したものである。
したがって、今回は、各配列から要素を取り出し和と差の計算を行う。
▼サンプルコード
# -*- Coding: UTF-8 -*-
# 多次元配列を変数に格納
A = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
B = [[9, 8, 7], [6, 5, 4], [3, 2, 1]]
# 計算結果格納用配列を用意
sum_val = []
sum_def = []
# 配列の要素数分ループ処理
for i in range(len(A)):
for j in range(len(A[i])):
# 和を算出し、配列に格納
sum_val.append(A[i][j] + B[i][j])
# 差を算出し、配列に格納
sum_def.append(A[i][j] - B[i][j])
# \nは改行コード
print("多次元配列の和:\n" + str(sum_val))
print("多次元配列の差:\n" + str(sum_def))
▼実行結果
多次元配列の和:
[10, 10, 10, 10, 10, 10, 10, 10, 10]
多次元配列の差:
[-8, -6, -4, -2, 0, 2, 4, 6, 8]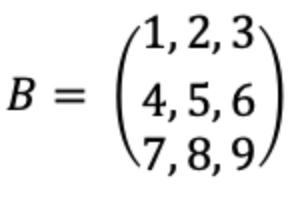

コメント