■多項式の微分計算
机上で多項式の微分計算を行う場合、以下の計算方法使用する。
▼微分計算
y = xnを微分すると、y’ = nxn-1
y = c (cは定数)を微分するとy’ = 0
▼例題
(1)関数 y = 2x3 – x2 + 4x – 7 を微分する。
y’ = 2・3x3-1 – 2・x2-1 + 4・1x1-1 – 0
y’ = 6x2 – 2x1 + 4x0
y’ = 6x2 – 2x1 + 4
(2)関数 y = (-3/2)x4 + x3 – x2 + x – (7/5) を微分する。
y’ = (-3/2)・4x4-1 + 3・x3-1 – 2・x2-1 + 1・x1-1– 0
y’ = -6x3 + 3x2 – 2x + 1
■pythonで微分を行う
pythonで微分を行う場合、sympy.limit()を使用する。
なお、sympy.limit()の使い方は以下を参照してください。
■例題
(1)関数 y = 2x3 – x2 + 4x – 7 を微分する
(2)関数 y = (-3/2)x4 + x3 – x2+ x – (7/5) を微分する
■サンプルコード
# -*- Coding:UTF-8 -*-
import sympy
# 関数:f(x) = 2x**3 - x**2 + 4x - 7
def f_1(x):
y_1 = (2 * x**3) - (x**2) + (4 * x) - 7
return y_1
# 関数:f(x) = -3/2x**4 + x**3 - x**2 + x - 7/5
def f_2(x):
y_2 = (-3/2) * x**4 + (x**3) - (x**2) + x - (7/5)
return y_2
if __name__ == '__main__':
# 文字列をセット
h = sympy.Symbol('h')
x = sympy.Symbol('x')
# 導関数を求める
result_1 = sympy.limit((f_1(x+h)-f_1(x))/h, h, 0)
result_2 = sympy.limit((f_2(x+h)-f_2(x))/h, h, 0)
# 計算結果を表示
print('問題1:', result_1)
print('問題2:', result_2)■実行結果
問題1: 6*x**2 - 2*x + 4
問題2: -6.0*x**3 + 3.0*x**2 - 2.0*x + 1.0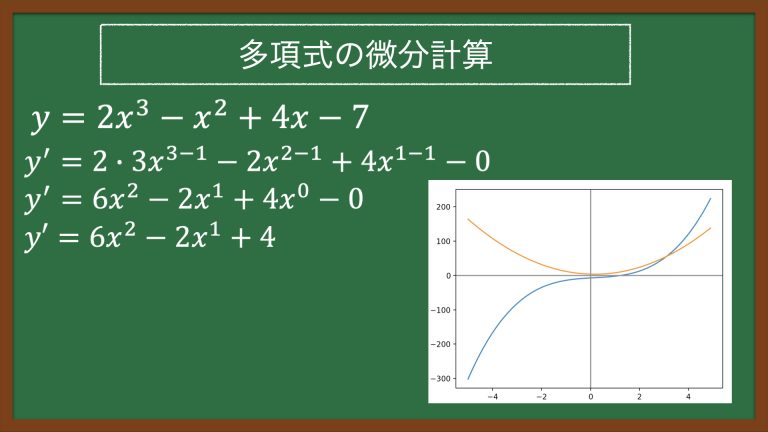
コメント