■概要
場合の数のうち、数珠順列について、
机上計算とPythonを使用した計算処理の2種類の解答方法を示す。
■数珠順列
下図のように、人以外のモノが円形に繋がっている場合は、ひっくり返すことが可能であり、このような順列を「数珠順列」と呼ぶ。
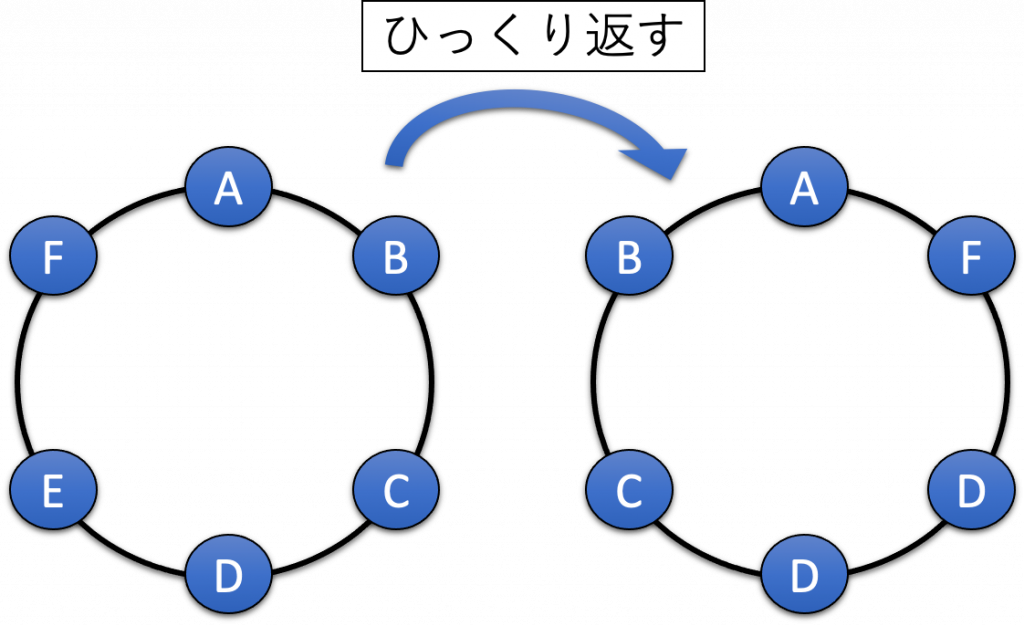
▼数珠順列の公式
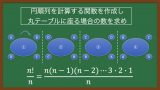
n個の異なる玉を繋いで円形に並べる場合は、「円順列 ÷ 2」で算出することができる。
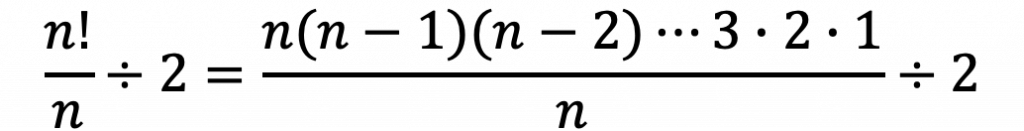
・参考:円順列の求め方
■例題
▼問1
6色の異なる玉で数珠を作成するときの場合の数を数を求める。
▼問2
8色の異なる玉から6個選び、数珠を作成するときの場合の数を求める。
■机上計算
▼問1
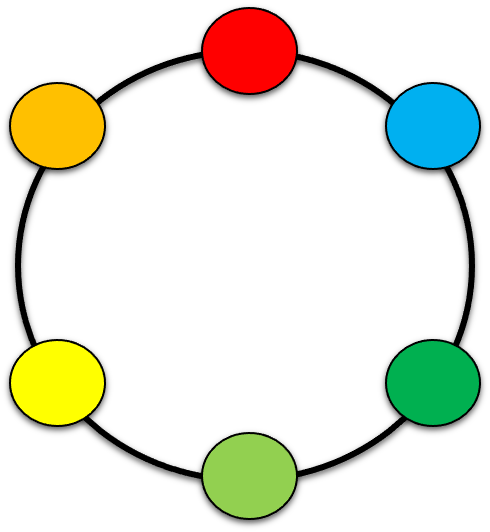
以下の図のように、6色の異なる玉で数珠を作る場合の数は、
(6!/ 6)/ 2
=(5!) / 2
= (5・4・3・2・1)/ 2
= 60(通り)
▼問2
以下の図のように、8色の異なる玉から6個選び、数珠を作る場合の数は、
①8個から6個選ぶ場合の数
8P6 通り
②円順列の計算(重複分の除去)
8P6 / 6 通り
③数珠順列の計算(ひっくり返し分の除去)
(8P6 / 6)/ 2
={(8・7・6・5・4・3・2・1)/ 6 } /2
=1680(通り)

■ Pythonによる実装
▼フローチャート
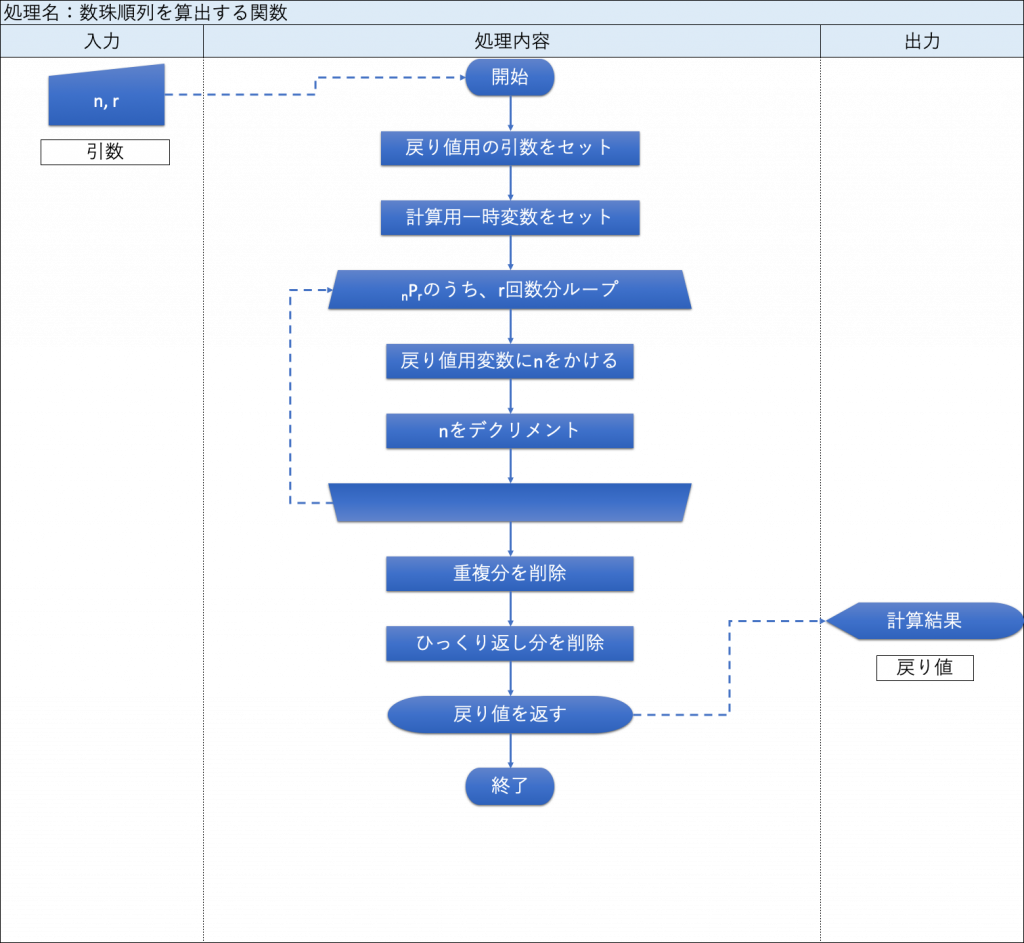
▼プログラム仕様
<処理名:数珠順列を計算する関数>
・引数と戻り値
| 項目 | 値 | 内容 |
|---|---|---|
| 第1引数 | n | n P r のうち、「n」 |
| 第2引数 | r | n P r のうち、「r」 |
| 戻り値 | 計算結果 | 数珠順列の計算結果 |
・処理概要
| 入力 | 処理内容 | 出力 |
|---|---|---|
| – | 戻り値用の初期値をセットする。 初期値:1 | – |
| – | 計算用の一時変数を用意する。 初期値:第一引数(n) | – |
| – | ■ n P r のうち、「r」の回数分ループ |戻り値用の値に「n」をかける。 |「n」を-1する。 ■ | – |
| – | 円順列として、重複分を削除する。 | – |
| – | 数珠順列として、ひっくり返し分を削除する。 | – |
| – | 戻り値として、計算結果を返す。 | 【戻り値】 計算結果 |
▼サンプルコード
# 数珠順列を算出する関数
def CalPrayerBeadsPermutation(n: int, r: int) -> int:
# 戻り値の初期値をセット
cal_data = 1
# 計算用一時変数
cal_tmp = n
# nPrのうち、r回数分ループする
for _ in range(r):
# nPrのうち、n(cal_tmp)で掛け算
cal_data = cal_data * cal_tmp
# デクリメント処理
cal_tmp = cal_tmp - 1
# 重複分を削除
cal_data = cal_data / r
# 円順列から重複分を削除
cal_data = cal_data / 2
# 戻り値を返す
return int(cal_data)
if __name__ == '__main__':
print('問1:', CalPrayerBeadsPermutation(7, 7), '通り')
print('問2:', CalPrayerBeadsPermutation(8, 6), '通り')
▼実行結果
問1: 360 通り
問2: 1680 通り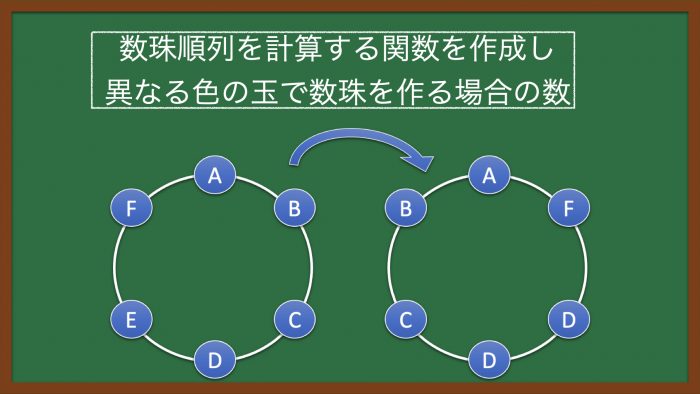


コメント