■概要
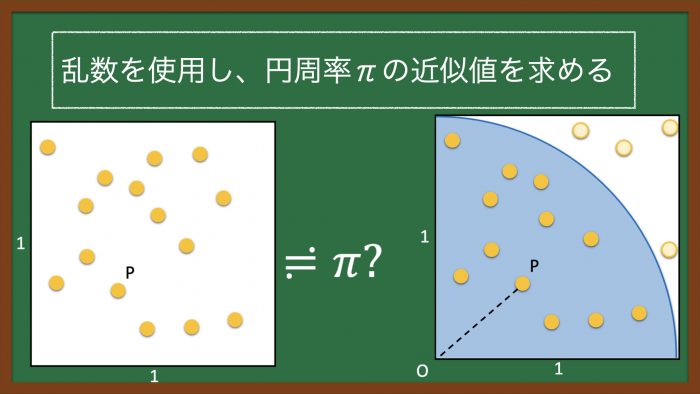
1×1の正方形の中に任意の点「P」を複数個プロットする。
プロットした任意の点「P」を使用して、円周率(π)の近似値を算出する。
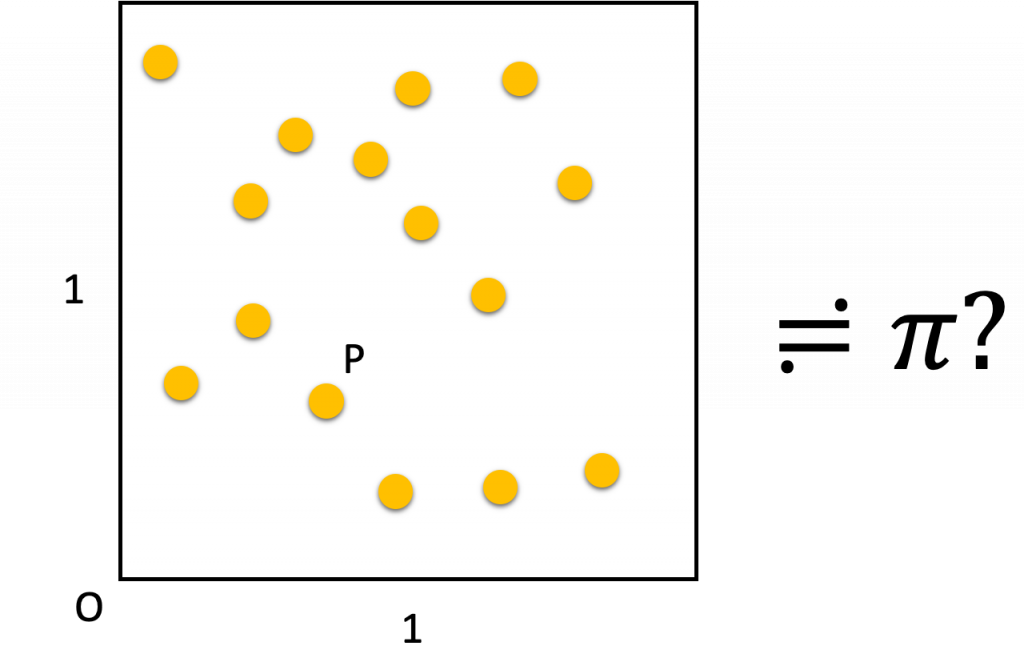
※オレンジ色の丸は任意にプロットした点「P」を示す
■乱数を使用した円周率πの近似値の求め方
「■概要」で示した1×1の正方形の中にプロットした、任意の点「P」を元に円周率の近似値の算出方法を示す。
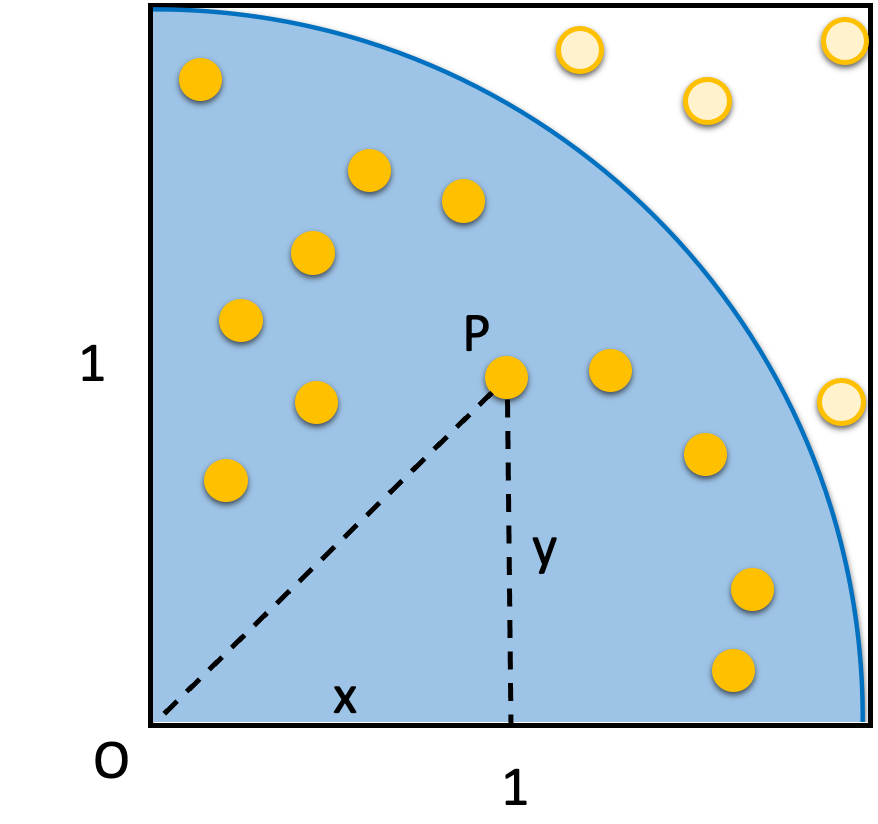
①1×1の正方形について、左下の角を中心とする円を作成する。
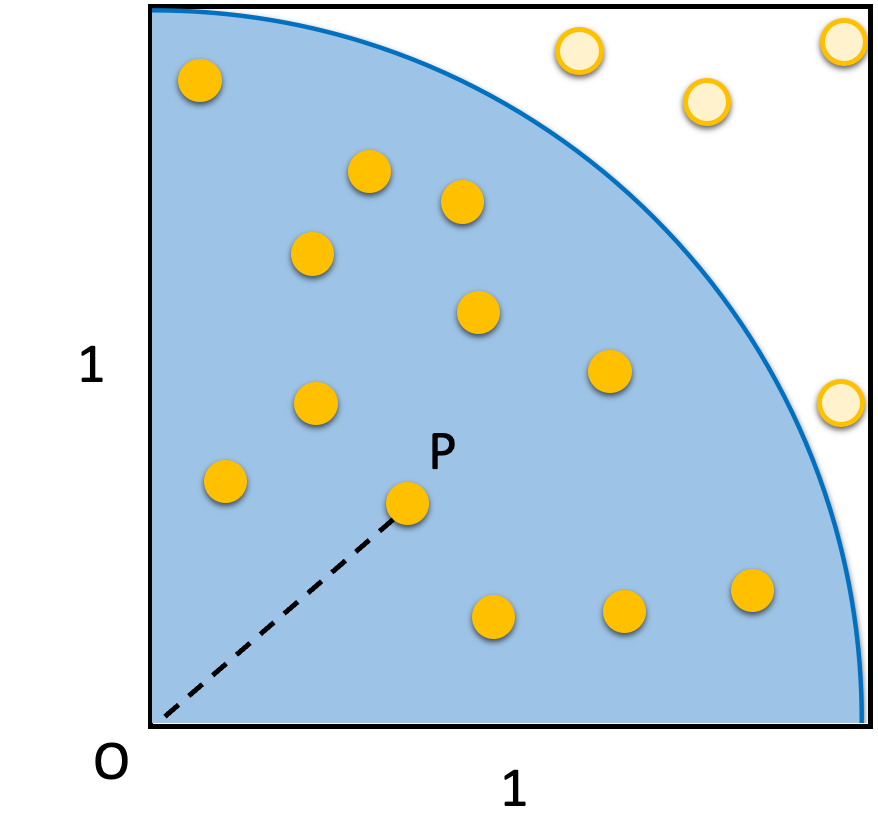
この時、1×1の正方形内に入っている点「P」の総数は、16個」であり、そのうち、円(水色)内に入っている点「P」の数は、12個である。
②1×1の正方形内に入っている点「P」の総数および円(水色)内に入っている点「P」の数を使用し、以下の公式に代入して計算すると・・・

おおよそ、円周率πに近しい値となる。
■Pythonによる実装
「■乱数を使用した円周率πの近似値の求め方」の図にて提示した、正方形内の点「P」の総数および円内の点「P」の数は、例として、意図的にプロットしたものとなる。
そこで、Pythonにて、任意の点「P」を乱数で設定した処理を実装し、円周率πの近似値となるか検証する。
また、プロットする任意の点「P」の総数も増やし、誤差の増減についても確認する。
▼フローチャート
「円周率の近似値を算出する関数」および「メイン処理」のフローチャートを示す。
・円周率の近似値を算出する関数
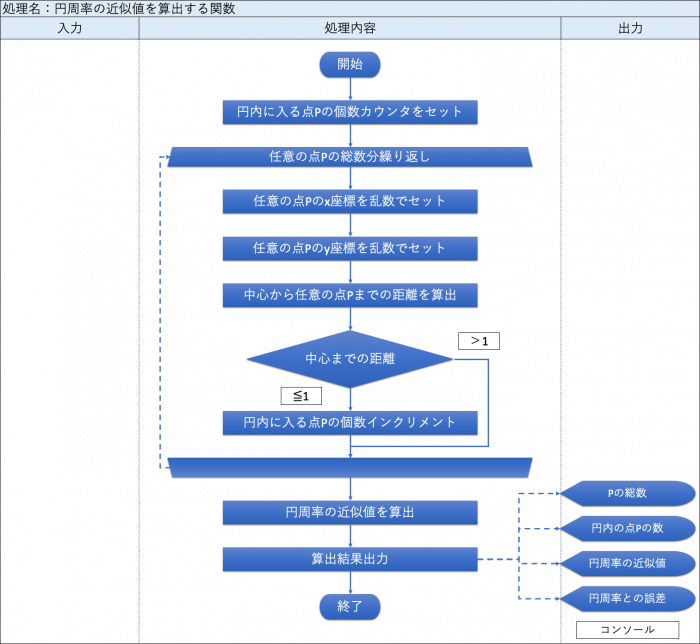
・メイン処理
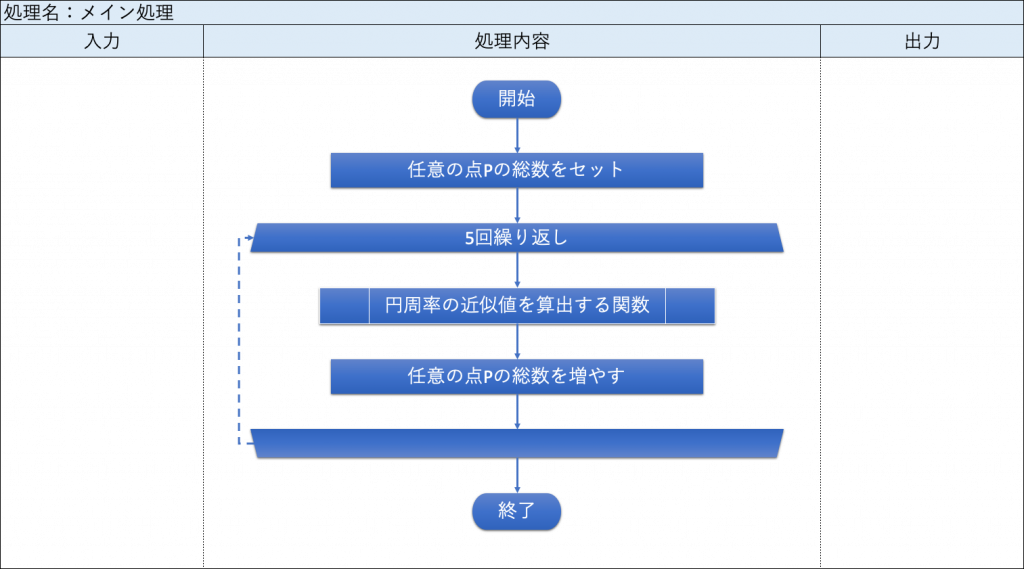
▼プログラム仕様
・円周率の近似値を算出する関数
「円周率の近似値を算出する関数」について、<引数と戻り値>および<処理内容>を下表に示す。
<引数と戻り値>
| 項目 | 型 | 項目内容 |
|---|---|---|
| 第1引数 | int型 | 任意の点Pの総数 |
| 戻り値 | – | なし |
<処理内容>
| 入力 | 処理内容 | 出力 |
|---|---|---|
| – | 円内に入る点Pの個数カウンタをセットする。 初期値:0 | – |
| – | ■ループ処理:任意の点Pの総数分繰り返し |任意の点Pのx座標を乱数でセットする。(0から1まで) |任意の点Pのy座標を乱数でセットする。(0から1まで) |中心から任意の点Pまでの距離を算出する。(三平方の定理) |▼条件分岐:中心から任意の点Pまでの距離(*) |【1以下の場合】 ||円内に入る点Pの個数カウンタをインクリメントする。 |▲ ■ | – |
| – | 円周率の近似値を算出する。 (4 × 円内の点Pの数)/ 正方形内の点Pの総数 | – |
| – | 算出結果を出力する。 | 【コンソール】 Pの総数 円内の点Pの数 円周率の近似値 円周率との誤差 |
(*)円内にプロットした点Pを判定する処理
プロットした点Pが半径「1」の円内に入っているかどうかは、中心「O」からの距離が「1」以内であるかどうかで判断可能である。
従って、三平方の定理を利用し、点Pのx座標とy座標の2乗の和が1以下であれば良い。
※「1」の2乗は「1」であるため、x座標とy座標の2乗の和が1以下かどうか確認すれば良い。
・メイン処理
「メイン処理」について、<引数と戻り値>および<処理内容>を下表に示す。
<引数と戻り値>
| 項目 | 型 | 項目内容 |
|---|---|---|
| 引数 | – | なし |
| 戻り値 | – | なし |
<処理内容>
| 入力 | 処理内容 | 出力 |
|---|---|---|
| – | 任意の点Pの総数をセットする。 初期値:1 | – |
| – | ■ループ処理:5回繰り返し |円周率の近似値を算出する関数呼び出し |任意の点Pの総数を増やす(10倍) ■ ※今回は、点Pの総数は、「1、10、100、1000、10000」とする。 | – |
▼サンプルコード
import math
import random
# 円周率の近似値を算出する関数
def chk_pi(P_sum):
# 円内に入る点Pの個数カウンタをセット
P_in_circle = 0
# 任意の点Pの総数分繰り返し
for _ in range(P_sum):
# 任意の点Pのx座標をセット(0から1まで)
tmp_x = random.random()
# 任意の点Pのy座標をセット(0から1まで)
tmp_y = random.random()
# 中心から任意の点Pまでの距離を算出(三平方の定理)
distance_from_origin = (tmp_x ** 2) + (tmp_y ** 2)
# 中心から任意の点Pまでの距離が1以下の場合、円内なのでカウント
if distance_from_origin <= 1:
P_in_circle += 1
# 円周率の近似値を算出
ans = (4 * P_in_circle) / P_sum
# 算出結果出力
print('Pの総数:', P_sum)
print('円内の点Pの数:', P_in_circle)
print('円周率の近似値:', ans)
print('円周率との誤差:', round(abs(ans - math.pi), 5))
# メイン処理
if __name__ == '__main__':
# 任意の点Pの総数をセット
p_sum = 1
# 5回繰り返す
for _ in range(5):
# 円周率の近似値を算出する関数呼び出し
chk_pi(p_sum)
# 任意の点Pの総数を増やす(10倍)
p_sum = p_sum * 10
▼実行結果
Pの総数: 1
円内の点Pの数: 1
円周率の近似値: 4.0
円周率との誤差: 0.85841
Pの総数: 10
円内の点Pの数: 7
円周率の近似値: 2.8
円周率との誤差: 0.34159
Pの総数: 100
円内の点Pの数: 86
円周率の近似値: 3.44
円周率との誤差: 0.29841
Pの総数: 1000
円内の点Pの数: 798
円周率の近似値: 3.192
円周率との誤差: 0.05041
Pの総数: 10000
円内の点Pの数: 7814
円周率の近似値: 3.1256
円周率との誤差: 0.01599■乱数を使用した円周率πの近似値の結果まとめ
下表に、Pythonにて、任意の点「P」を乱数で設定した処理の実行結果をまとめたものを示す。

点Pの総数が多くなるにつれて、円周率(3.14・・・)に近くなっていくことがわかる。


コメント