■合成関数
合成関数とは、2つの関数 f(x) および g(x) について、一方の変数 x にもう一方の関数をまるごと代入したもの。
▼合成関数の表記方法
f(g(x)) ←→ f○g(x)
g(f(x)) ←→ g○f(x)
▼合成関数の性質
f○g ≠ g○f
f○(g○h) = (f○g)○h
■例題
f(x) = x + 1、g(x) = x2、h(x) = x – 3 のとき、次の関数を求める。
問題1:f○g(x)
問題2:g○f(x)
問題3:f○(g○h)
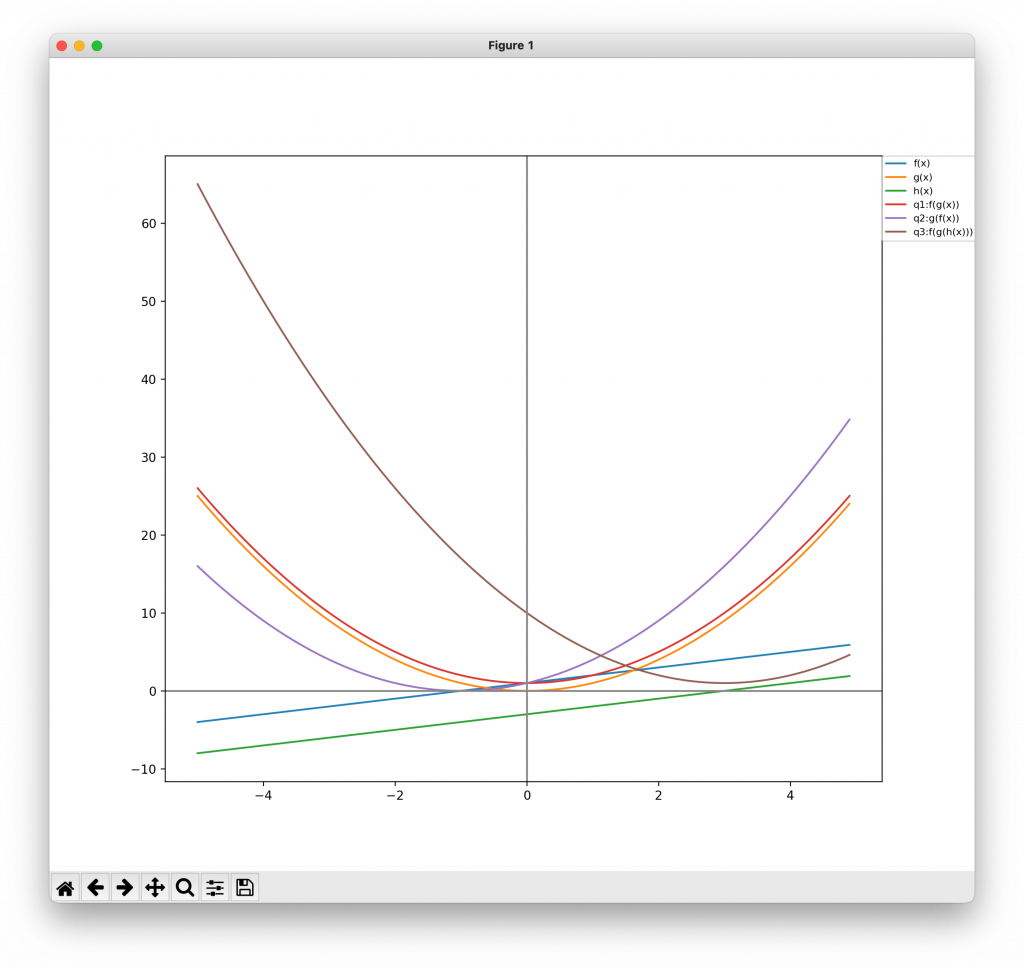
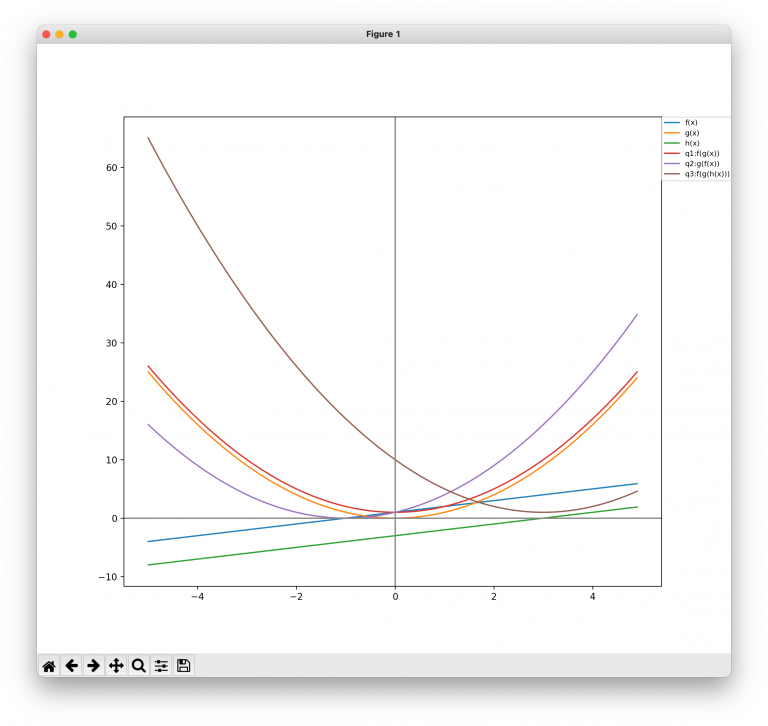
また、f(x)、g(x)、h(x)、問題1、問題2、問題3のグラフを図示する。
■サンプルコード(問題1から3)
# -*- Coding:UTF-8 -*-
import sympy
# f(x) = x + 1
def f(x):
return x + 1
# g(x) = x**2
def g(x):
return x ** 2
# h(x) = x - 3
def h(x):
return x - 3
if __name__ == '__main__':
# 文字列をセット
x = sympy.Symbol('x')
# 問題1:f○g(x) = f(g(x))
print('問題1:', f(g(x)))
# 問題2:g○f(x) = g(f(x))
print('問題2:', g(f(x)))
# 問題3:f○(g○h) = f(g(h(x)))
print('問題3:', f(g(h(x))))
▼実行結果
問題1: x**2 + 1
問題2: (x + 1)**2
問題3: (x - 3)**2 + 1■サンプルコード(グラフに図示)
# -*- Coding: UTF-8 -*-
import numpy as np
from matplotlib import pyplot as plt
# xの値を便宜上、0.1間隔で -5 < x < 5 の範囲を指定
xmin = -5
xmax = 5
xinterval = 0.1
x = np.arange(xmin, xmax, xinterval)
# f(x) = x + 1を算出
f = x + 1
# f(x) = x + 1をグラフに図示
plt.plot(x, f, label = "f(x)")
# g(x) = x**2 を算出
g = x**2
# g(x) = x**2 をグラフに図示
plt.plot(x, g, label = "g(x)")
# h(x) = x - 3 を算出
h = x - 3
# g(x) = x - 3 をグラフに図示
plt.plot(x, h, label = "h(x)")
# 問題1:f(g(x)) = x**2 + 1 を算出
q1 = x**2 + 1
# f(g(x)) = x**2 + 1 をグラフに図示
plt.plot(x, q1, label = "q1:f(g(x))")
# 問題2:g(f(x)) = (x + 1)**2 を算出
q2 = (x + 1)**2
# g(f(x)) = (x + 1)**2 をグラフに図示
plt.plot(x, q2, label = "q2:g(f(x))")
# 問題3: f(g(h(x))) = (x - 3)**2 + 1 を算出
q3 = (x - 3)**2 + 1
# f(g(h(x))) = (x - 3)**2 + 1 をグラフに図示
plt.plot(x, q3, label = "q3:f(g(h(x)))")
# ラベルの表示
plt.legend(bbox_to_anchor=(1, 1), loc='upper left', borderaxespad=0, fontsize=8)
########## グラフにx軸,y軸(0)を図示 ##########
# 補助線(0)を作成 [axhline:水平 axvline:垂直]
plt.axhline(y = 0, color = "gray")
plt.axvline(x = 0, color = "gray")
############################################
# グラフを表示
plt.show()
▼実行結果


コメント