■積立預金の元利合計(複利)
積立預金の元利合計(複利)の算出は以下のように計算していく。
▼(例)毎年4万円ずつ年利4%で5年間積み立てた場合
1年目:40000円 × 1.04 = 41600円
2年目:(41600円 + 40000円) × 1.04 = 84864円
3年目:(84864円 + 40000円) × 1.04 = 129858.56円
4年目:(129858.56円 + 40000円) × 1.04 = 176652.9024円
5年目:(176652.9024円 + 40000円) × 1.04 = 225319.018496円
▼イメージ図
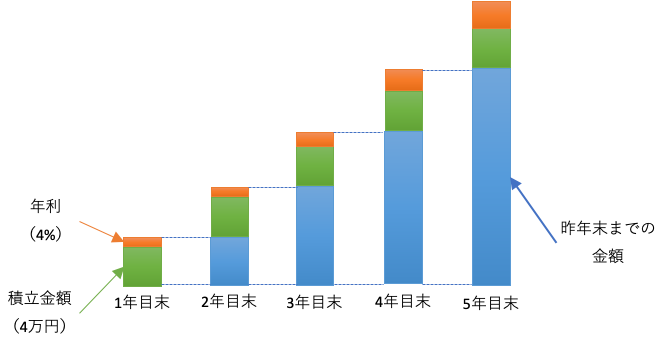
複利の場合、2年目以降は「昨年末の金額(積み立て金額+年利)」と「積立金額(4万円)」の合計金額に年利が適応されるため、各年の年利額は増えていく。
また、積立預金の元利合計(複利)の算出は、等比数列の和の公式を応用して算出することができる。
▼a:積立金額(円)、r:年利(%)、n:年数のときの元利合計(Sn)は以下の通りである。

▼参考(等比数列の和)
■例題
毎年4万円ずつ年利4%で5年間積み立てた場合の元利合計金額を求める。
※小数点以下は切り捨てる
■サンプルコード
# -*- Coding:UTF-8 -*-
import math
# 積立預金の元利合計を算出するメソッド
def TsumitateYokin(a:int, r:int, n:int) -> int:
# 等比数列の和の公式:
# (a/r)*(1+r)*{(1+r)**n-1}
ans = (a / r) * (1 + r) * ((1 + r)**n - 1)
# 小数点以下は切り捨て
return math.floor(ans)
if __name__ == '__main__':
# 毎年4万円ずつ年利4%で5年間積み立てた場合
a = 40000
r = 0.04
n = 5
# 積立預金の元利合計を算出するメソッドを呼び出し
result = TsumitateYokin(a, r, n)
# 計算結果を出力
print(result)
■実行結果
225319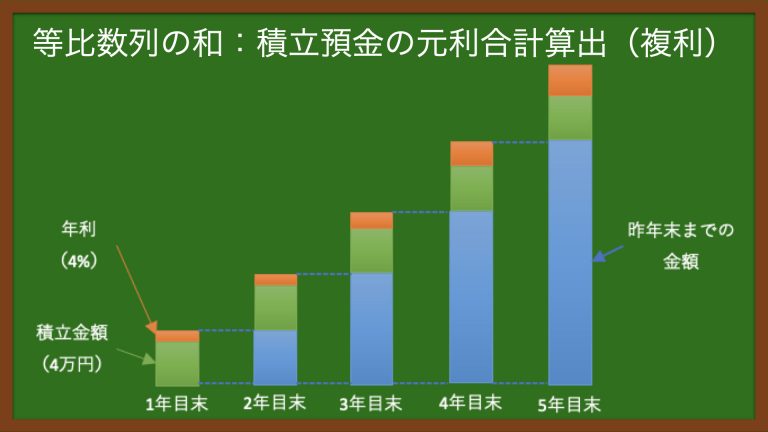


コメント