■概要
場合の数のうち、順列に関する問題を解く。
なお、机上による計算方法と、Pythonを使用してプログラミングで解く方法の2種類を示す。
■順列
順列(Permutation)とは、ある事象を並び替えた時、順番が異なれば、全く別の事象としてカウントする。
例:「1、2、3」の3つの整数から3桁の数字を作成すると、以下の6通りとなる。
「123」、「132」、「213」、「231」、「312」、「321」
順列は、「n P r」と表記し、「Pのn、r」と読む。
n:n個の中から
r:r個選ぶ
▼順列の計算方法
順列「n P r」を計算する方法を以下に示す。
イメージとしては、r回数分1ずつnを引き算し、掛け算していくと考えておけば問題なし。
公式:n P r = n × (n – 1)×(n – 2)×・・・×(n – r + 1)
例:「1、2、3」の3つの整数から3桁の数字を作成する。
3 P3 = 3 ×(3 – 1)×(3 – 2)= 3 × 2 × 1 = 6(通り)
なお、n = r であるとき「n P n」は、「n!」と表記し、「nの階乗(かいじょう)」と読む。
■例題
▼問1
「1、2、3、4、5」の5つの整数から3桁の数字を作成する。
▼問2
親2人と子ども3人の計5人が1列に並ぶ並び方について、以下の場合の数を求める。
問2-1
5人全員の並び方は、全部で何通りあるか。
問2-2
親2人が両端であり、その間に子ども3人が入る並び方は何通りあるか。
■机上計算
▼問1
「1、2、3、4、5」の5つの整数から3桁の数字を作成すると、
「123」、「124」、「125」・・・
と表すことができる。
この時、
百の位に入る数字は「1、2、3、4、5」の5通り。
十の位に入る数字は、百の位の場合の数から「-1」して4通り。
一の位に入る数字は、十の位の場合の数から「-1」して3通り。
従って、求める場合の数は、
5P3 = 5 × 4 × 3 = 60(通り)
▼問2
・問2-1
親2人と子ども3人の計5人が1列に並ぶ並び方については、


:
と表すことができる。
この時、
1番目に入る場合の数は、5人いるので5通り。
2番目に入る場合の数は、1番目で1人選んでいるので4通り。
3番目に入る場合の数は、2番目で1人選んでいるので3通り。
4番目に入る場合の数は、3番目で1人選んでいるので2通り。
5番目に入る場合の数は、4番目で1人選んでいるので1通り。
従って、求める場合の数は、
n! = 5P5 = 5 × 4 × 3 × 2 × 1 = 120(通り)
・問2-2
親2人が両端であり、その間に子ども3人が入る並び方は、以下の表のように示すことができる。


:
と表すことができる。
この時、
・2人の親を両端に並べる場合の数は、
左端に1人を選ぶ場合の数は、2通り。
右端に1人を選ぶ場合の数は、左端に1人選んでいるので1通り。
・3人の子どもを間に並べる場合の数は、
3人の中から1人選ぶので、3通り。
次に2人の中から1人選ぶので、2通り。
最後に1人の中から1人選ぶので、1通り。
従って、求める場合の数は、
2 P 2 × 3 P 3
= (2 × 1) × (3 × 2 × 1)
= 2 × 6
= 12(通り)
■Pythonによる実装
▼フローチャート
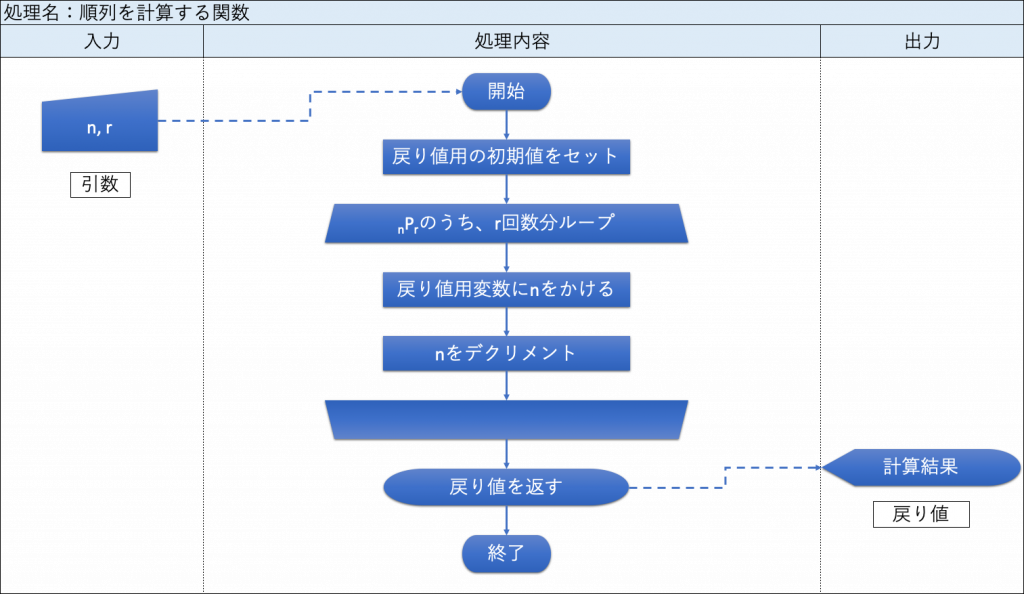
▼プログラム仕様
<処理名:順列を計算する関数>
・引数と戻り値
| 項目 | 値 | 内容 |
|---|---|---|
| 第1引数 | n | n P r のうち、「n」 |
| 第2引数 | r | n P r のうち、「r」 |
| 戻り値 | 計算結果 | n P r の計算結果 |
・処理概要
| 入力 | 処理内容 | 出力 |
|---|---|---|
| – | 戻り値用の初期値をセットする。 初期値:1 | – |
| – | ■ n P r のうち、「r」の回数分ループ |戻り値用の値に「n」をかける。 |「n」を-1する。 ■ | – |
| – | 戻り値として、計算結果を返す。 | 【戻り値】 計算結果 |
▼サンプルコード
# 順列を計算する関数
def cal_permutation(n: int, r: int) -> int:
# 戻り値の初期値をセット
result = 1
# nPrのうち、r回数分ループする
for _ in range(r):
# nPrのうち、nで掛け算
result = result * n
# デクリメント処理
n = n - 1
# 戻り値を返す
return result
if __name__ == '__main__':
# 問1
print('問1:', cal_permutation(5, 3), '通り')
# 問2-1
print('問2-1:', cal_permutation(5, 5), '通り')
# 問2-2
parents_patern = cal_permutation(2, 2)
children_patern = cal_permutation(3, 3)
ans = parents_patern * children_patern
print('問2-2:', ans, '通り')
▼実行結果
問1: 60 通り
問2-1: 120 通り
問2-2: 12 通り

コメント