■概要
「速さ」と「速度」は物理では別物として扱う。
「速さ」と「速度」の違いを説明し、それぞれの机上とPythonで計算を行う。
■速さ
速さは値の大きさを表すものであり、「距離÷時間」で求めることができる。
すなわち、単位時間あたり、どのくらいの距離を進んだかを速さとしている。
なお、大きさだけを考えるものをスカラーと呼ぶ。
速さの単位は、距離(km、mなど)と時間(時間:h、秒:sなど)の単位に依存する。
例えば、距離(m)あたりの時間(秒:s)の場合は、「m/s」と表す。
▼問1
50mの距離を10秒で走る時、以下の2問を求める。
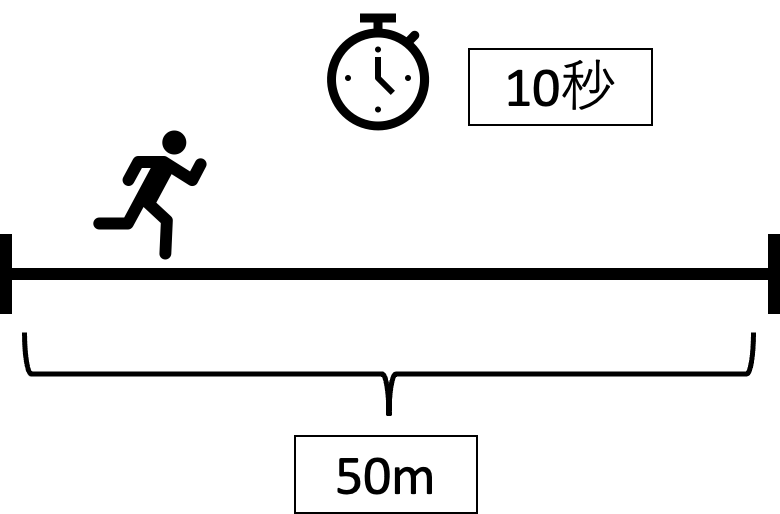
・問1-1:速さ(m/s)を求める。
速さ(m/s)
= 50(m)÷ 10(秒:s)
= 5.0(m/s)
・問1-2:速さ(km/h)を求める。
まず、距離「m」を「km」、時間「s」を「h」に変換する必要がある。
1(m) = 1/1000(km)
1(s) = 1/3600(h)
速さ(km/h)
=(50(m)÷ 1000)÷ (10(s)÷ 3600)
= 18(km/h)
■平均の速さ
前項の「■速さ」の問1では、一定の距離を同じ時間で移動したと仮定し、速さを算出したが、途中で速さが変わった場合の平均の速さは、それぞれの速さの平均ではなく、全体の距離とかかった時間で求める。
▼問2
80mの距離を最初の30mは30秒で歩き、残りの50mは10で走った場合の平均の速さ(m/s)を求める。
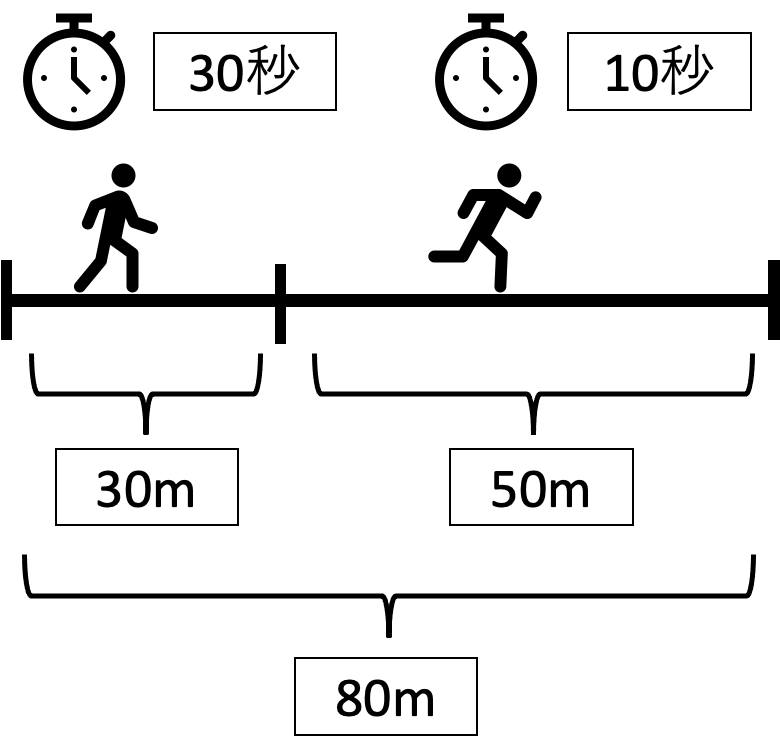
まず、全体の距離とかかった時間を算出し、それぞれで速さを求める。
速さ(m/s)
= (30(m)+ 50(m))÷(30(s)+ 10(s))
= 80(m) ÷ 40(s)
= 2.0(m/s)
■速度
「速さ」は大きさだけで表すのに対して、「速度」は大きさと向きで表す。
なお、速度のように、大きさと向きで表すものをベクトルと呼ぶ。
速度を表す場合、任意の方向AからBへ進む場合を「正」とした時、任意の方向BからAへ進む場合を「負」とする。
▼問3
西から東へ進む方向を「正」としたとき、西から東へ3.0(m/s)の速さで移動する場合と、東から西へ2.0(m/s)の速さで移動する場合の速度を求める。
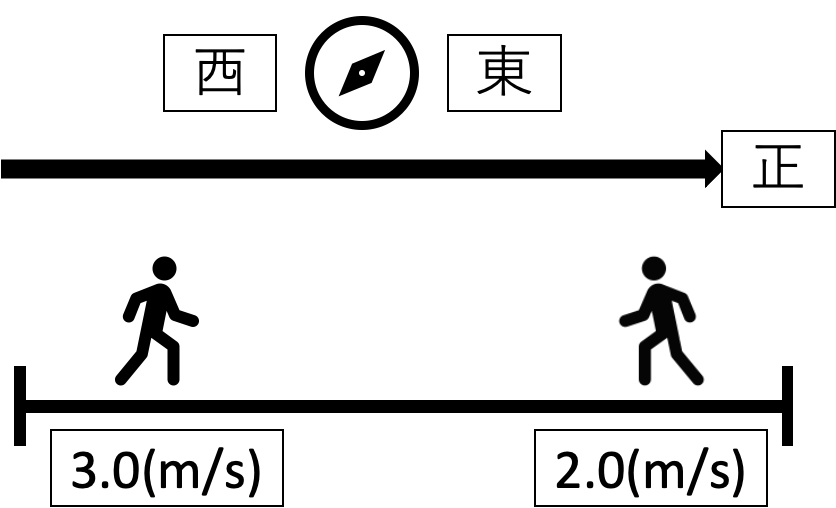
西から東へ進む方向を「正」とした場合、
3.0(m/s)
-2.0(m/s)
と表すことができる。
■Pythonによる実装
問1から問3までの問題について、Pythonによる計算を示す。
▼サンプルコード
# 速さ(m/s)を算出する関数
def cal_speed_m_s(m, s):
return m / s
# 距離(m)と時間(s)から、速さ(km/h)を算出する関数
def cal_speed_m_s_to_km_h(m, s):
# mをkmに変換
km = m / 1000
# s(秒)をh(時間)に変換
h = s / 3600
return km / h
# 速さと正負から速度に変換する関数
def change_positive_nagative(m_s, flg):
# flg:Trueの場合は正の速度
if flg:
return m_s
# flg:Falseの場合は負の速度
else:
return -1 * m_s
# メイン処理
if __name__ == '__main__':
# 問1:50mの距離を10秒で走る場合
m = 50
s = 10
# 問1-1:速さ(m/s)
print('問1-1:', cal_speed_m_s(m, s), 'm/s')
# 問1-2:速さ(km/h)
print('問1-2:', cal_speed_m_s_to_km_h(m, s), 'km/h')
# 問2:80mの道のりを最初の30mは30秒で歩き
# 残りの50mは10秒で走る場合の平均の速さ
m = 30 + 50
s = 30 + 10
print('問2:', cal_speed_m_s(m, s), 'm/s')
# 問3:西から東へ向かう場合を正とした場合
# 西から東:True
# 東から西:False
# 問3-1:西から東へ3.0m/sの速度
print('問3-1:', change_positive_nagative(3.0, True), 'm/s')
# 問3-2:東から西へ2.0m/sの速度
print('問3-2:', change_positive_nagative(2.0, False), 'm/s')▼実行結果
問1-1: 5.0 m/s
問1-2: 18.0 km/h
問2: 2.0 m/s
問3-1: 3.0 m/s
問3-2: -2.0 m/s

コメント