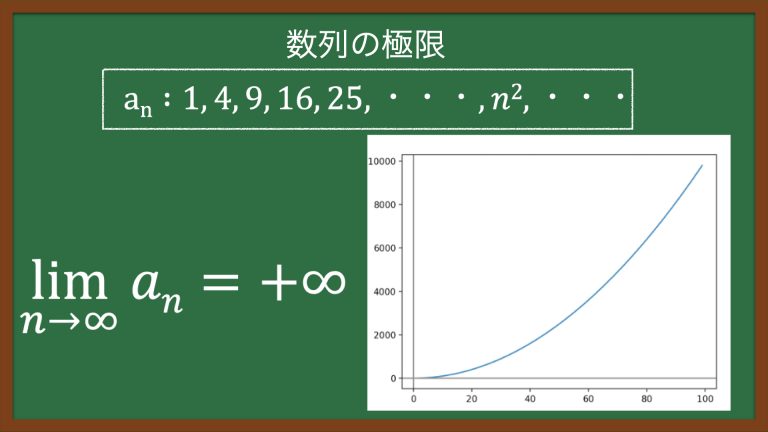
■数列の極限
数列の極限とは、数列に対して、1番目の値→2番目の値・・・100番目の値と、項数を増やしていったとき、明確な結果が出る場合を「極限がある」と呼び、明確な結果が出ない場合を「極限がない」と表す。
▼極限の種類
・数列an:1、2、3、・・・、n、・・・
・数列bn:-3、-6、-9、・・・、-3n、・・・
・数列cn:-5、25、-125、・・・、-5n、・・・
・数列dn:1/4、1/16、1/64、・・・、(1/4)n、・・・
数列anは、徐々に数が大きくなり、キリがなく無限に増加している。
この状態を正の無限大に発散すると呼び、以下の式で表すことができる。

また、数列anは、明確な結果(+∞)が出ているため、「極限がある」に分類される。
数列bnは、徐々に数が小さくなり、キリがなく無限に減少している。
この状態を負の無限大に発散すると呼び、以下の式で表すことができる。

また、数列bnは、明確な結果(-∞)が出ているため、「極限がある」に分類される。
数列cnは、交互に正負の値となり、一定の値に収束することがない。この状態のことを振動と呼ぶ。
また、数列bnは、明確な結果が出ないため、「極限がない」に分類される。
数列dnは、徐々に数が小さくなり、限りなく0に近づいている。
この状態をを0に収束すると呼び、以下の式で表すことができる。

数列dnは、明確な結果(0)が出ているため、「極限がある」に分類される。
また、一定の値(数列dnでは0)に近く場合、その値を極限値と呼ぶ。
▼極限の種類(まとめ)
極限について、数列anからdnまでをまとめた表を以下に示す。
| 数列 | 極限の有無 | 収束/発散 | 極限値 |
|---|---|---|---|
| an | 極限がある | 発散 | – |
| bn | 極限がある | 発散 | – |
| cn | 極限がない | 発散 | – |
| dn | 極限がある | 収束 | 0 |
■例題
pythonのsympy.limit()を使用して極限を求める。
▼sympy.limit()の使い方
Pythonのsympy.limit()を使用することで、極限の有無・極限値を算出してくれる。
▼使い方
limの式について、それぞれ引数を設定していく。
sympy.limit(求める式, 任意の変数(n), 無限(∞))
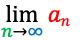
▼問題1
・問題

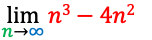
・サンプルコード
import sympy
# 文字列をセット
n = sympy.Symbol('n')
# 無限をセット
oo = sympy.oo
# 問題1を解く
ans1 = sympy.limit((n**3) - (4 * (n**2)), n, oo)
# 結果を表示
print(ans1)・実行結果
oo・補足:グラフに図示して確認
import numpy as np
from matplotlib import pyplot as plt
# 便宜上、第1から100項までの値を設定
n_min = 1
n_max = 100
n_interval = 1
n = np.arange(n_min, n_max, n_interval)
# 数列a(n)について、第1から100項までの値を算出
an = (n**3) - (4 * (n**2))
# グラフを作成
plt.plot(n, an)
# グラフにx軸,y軸(0)を図示
# 補助線(0)を作成 [axhline:水平 axvline:垂直]
plt.axhline(y=0, color="gray")
plt.axvline(x=0, color="gray")
# グラフを表示
plt.show()
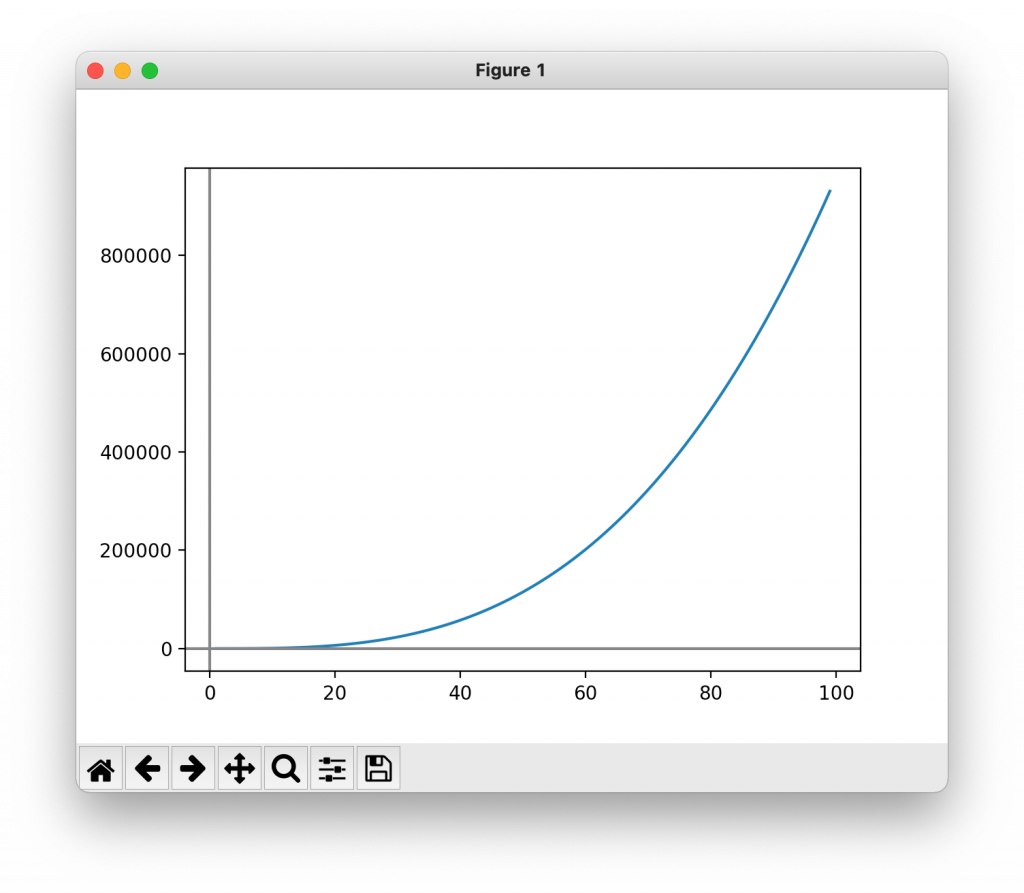
∞に増加し続けていることがわかる。
▼問題2
・問題

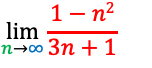
・サンプルコード
import sympy
# 文字列をセット
n = sympy.Symbol('n')
# 無限をセット
oo = sympy.oo
# 問題2を解く
ans2 = sympy.limit((1 - (n**2))/((3 * n) + 1), n, oo)
# 結果を表示
print(ans2)・実行結果
-oo・補足:グラフに図示して確認
import numpy as np
from matplotlib import pyplot as plt
# 便宜上、第1から100項までの値を設定
n_min = 1
n_max = 100
n_interval = 1
n = np.arange(n_min, n_max, n_interval)
# 数列b(n)について、第1から100項までの値を算出
bn = (1 - (n**2))/((3 * n) + 1)
# グラフを作成
plt.plot(n, bn)
# グラフにx軸,y軸(0)を図示
# 補助線(0)を作成 [axhline:水平 axvline:垂直]
plt.axhline(y=0, color="gray")
plt.axvline(x=0, color="gray")
# グラフを表示
plt.show()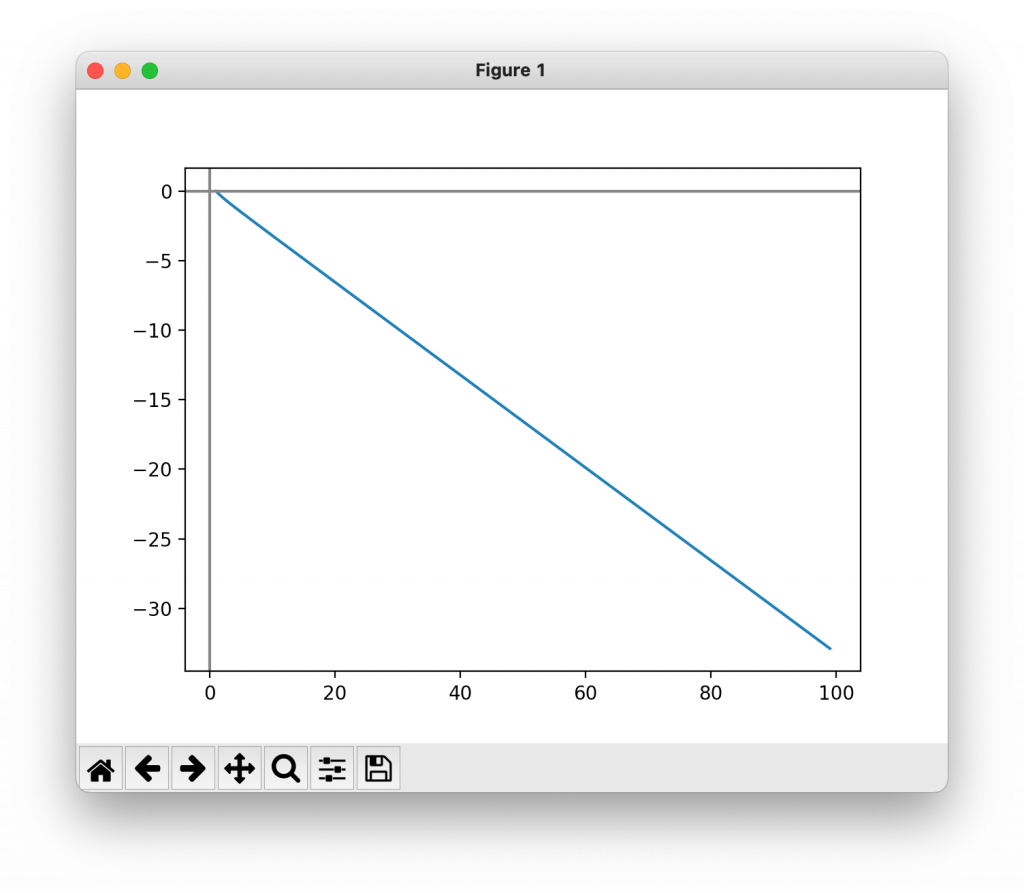
∞に減少し続けていることがわかる。
▼問題3
・問題

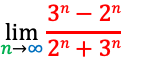
・サンプルコード
import sympy
# 文字列をセット
n = sympy.Symbol('n')
# 無限をセット
oo = sympy.oo
# 問題3を解く
ans3 = sympy.limit(((3**n) - (2**n))/((2**n) + (3**n)), n, oo)
# 結果を表示
print(ans3)・実行結果
1・補足:グラフに図示して確認
import numpy as np
from matplotlib import pyplot as plt
# 便宜上、第1から30項までの値を設定
n_min = 1
n_max = 30
n_interval = 1
n = np.arange(n_min, n_max, n_interval)
# 数列c(n)について、第1から30項までの値を算出
cn = ((3**n) - (2**n))/((2**n) + (3**n))
# グラフを作成
plt.plot(n, cn)
# グラフにx軸,y軸(0)を図示
# 補助線(0)を作成 [axhline:水平 axvline:垂直]
plt.axhline(y=0, color="gray")
plt.axvline(x=0, color="gray")
# グラフを表示
plt.show()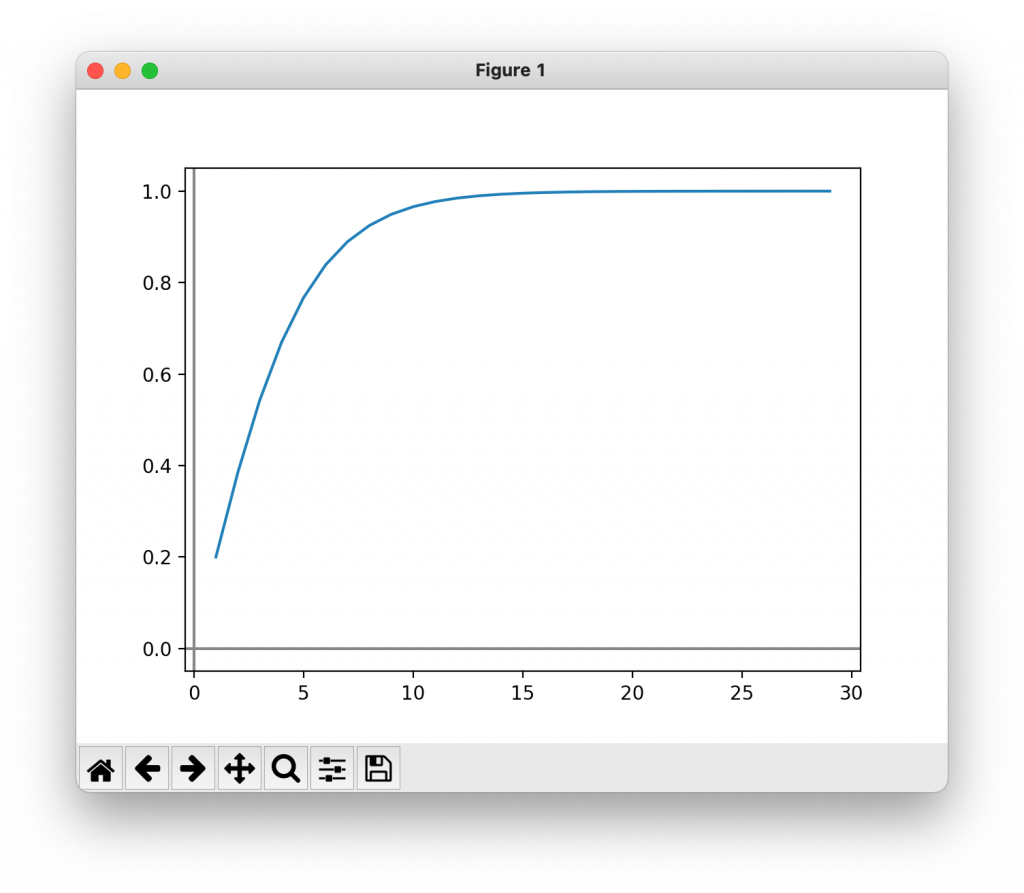
1に収束していることがわかる。
▼問題4
・問題
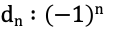
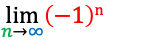
・サンプルコード
import sympy
# 文字列をセット
n = sympy.Symbol('n')
# 無限をセット
oo = sympy.oo
# 問題4を解く
ans4 = sympy.limit((-1)**n, n, oo)
# 結果を表示
print(ans4)・実行結果
nan極限がない場合は「nan」が返される。
・補足:グラフに図示して確認
import numpy as np
from matplotlib import pyplot as plt
# 便宜上、第1から10項までの値を設定
n_min = 1
n_max = 10
n_interval = 1
n = np.arange(n_min, n_max, n_interval)
# 数列d(n)について、第1から10項までの値を算出
dn = (-1)**n
# グラフを作成
plt.plot(n, dn)
# グラフにx軸,y軸(0)を図示
# 補助線(0)を作成 [axhline:水平 axvline:垂直]
plt.axhline(y=0, color="gray")
plt.axvline(x=0, color="gray")
# グラフを表示
plt.show()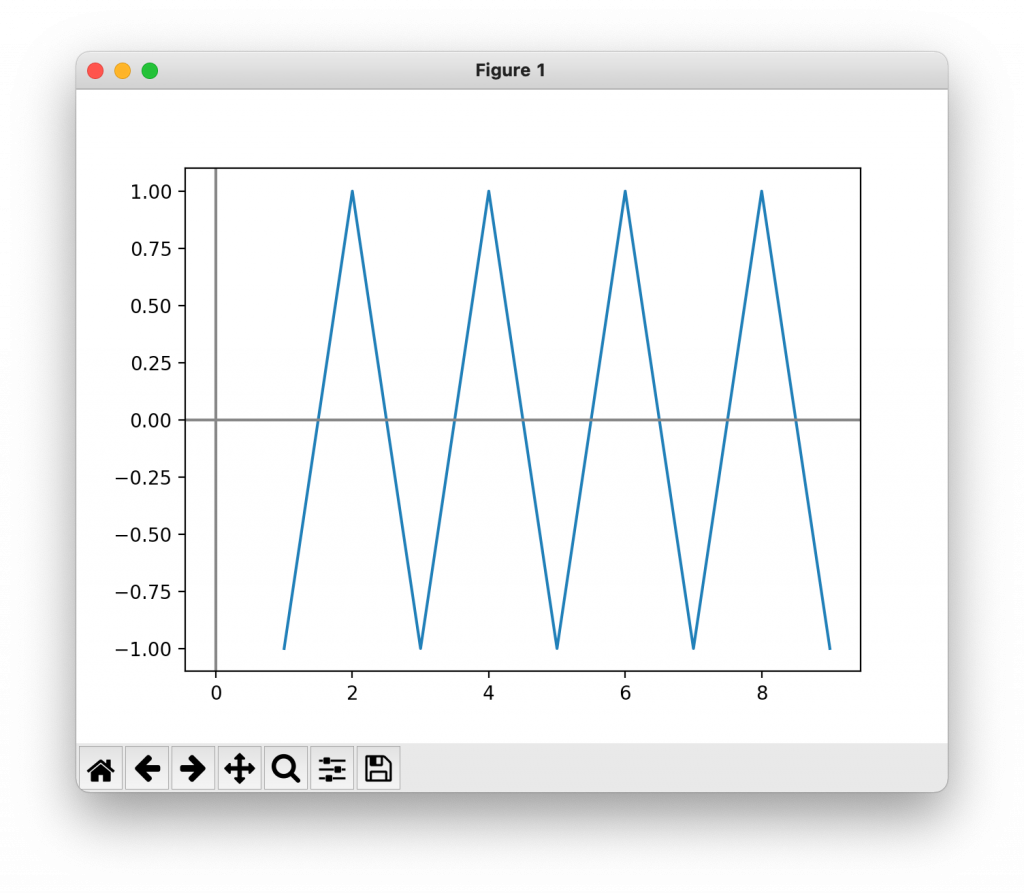
1と-1を行きき(振動)しており、収束していないことがわかる。


コメント