■累乗
累乗とは、自分自身を何回も(n回)掛け算したものであり、anと表す。
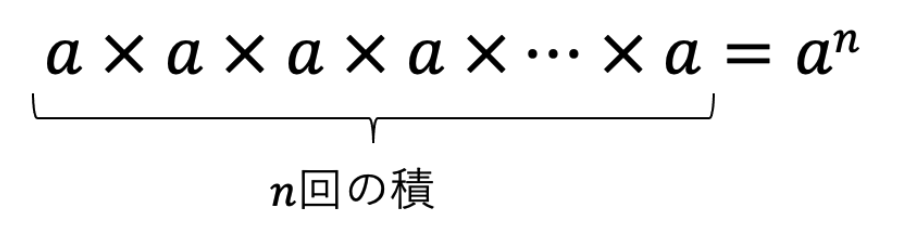
この時、anのaを底、nを指数と表す。

■指数の法則 その1
x > 0
y > 0
m、n は有理数
・・・の場合、以下の法則が成り立つ。
指数の法則①
底が同じ場合、指数は足算できる。
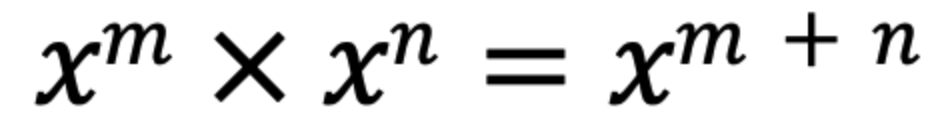
指数の法則②
底が同じ場合、指数は引き算できる。
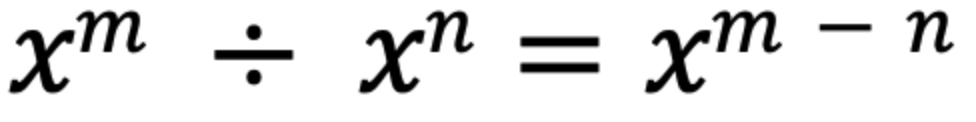
指数の法則③
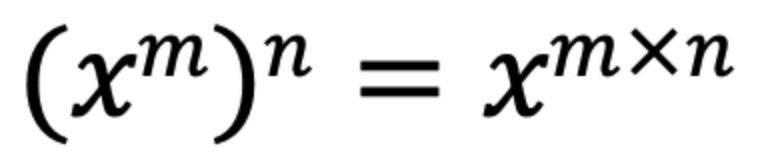
指数の法則④
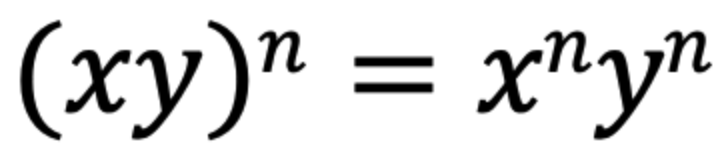
▼例題
以下の問題をpythonを使って表示する。
(x > 0 および y > 0とする)
問題1

問題2
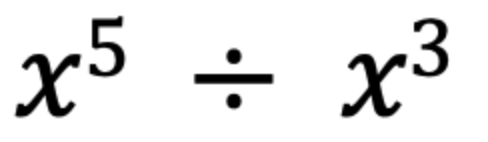
問題3
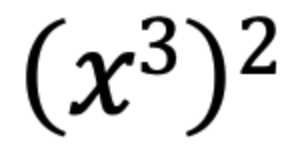
問題4
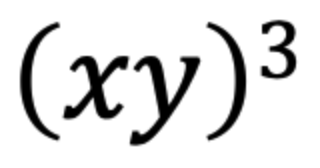
▼サンプルコード
# -*- Coding:UTF-8 -*-
import sympy
if __name__ == '__main__':
# 文字列をセット
x = sympy.Symbol('x')
y = sympy.Symbol('y')
# 問題1
print('問題1:', (x ** 2) * (x ** 3))
# 問題2
print('問題2:', (x ** 5) / (x ** 3))
# 問題3
print('問題3:', (x ** 3) ** 2)
# 問題4
print('問題4:', (x * y) ** 3)
▼実行結果
問題1:x**5
問題2:x**2
問題3:x**6
問題4:x**3*y**3※pythonでは、累乗は[**]で表す
■指数の法則 その2
x > 0
y > 0
n は自然数
・・・の場合、以下の法則が成り立つ。
指数の法則⑤

指数の法則⑥

指数の法則⑦

指数の法則⑧
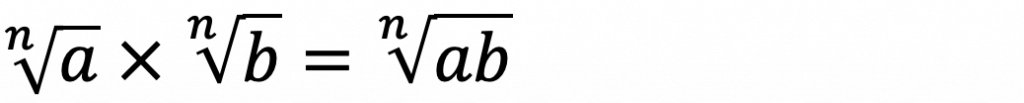
▼例題
以下の問題をpythonを使って表示する。
(x > 0 および y > 0とする)
問題5

問題6

問題7

問題8
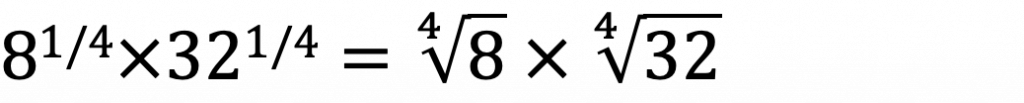
▼サンプルコード
# -*- Coding:UTF-8 -*-
import sympy
if __name__ == '__main__':
# 文字列をセット
x = sympy.Symbol('x')
y = sympy.Symbol('y')
# 問題5
print('問題5:', (x ** 0))
# 問題6
print('問題6:', (x ** -1))
# 問題7
print('問題7:', (8 ** 1/4))
# 問題8
print('問題8:', (8 ** 1/4) * (32 ** 1/4))
▼実行結果
問題5: 1
問題6: 1/x
問題7: 2.0
問題8: 16.0
コメント