■常用対数
常用対数とは、底を10とする log10x で表記される。
一般的に、常用対数は、log102 = 0.3010、log103 = 0.4771として、整数の桁数および小数点の位置を調べるのに便利である。
今回はlog102 = 0.3010、log103 = 0.4771を使用せず、Pythonのmath.log()メソッドを使用して問題を解く。
■例題
以下の常用対数をPythonのmath.log()メソッドを使用して求める。
▼問題1
log106
▼問題2
log1018
▼問題3(応用)
log38
※問題3については、そのままPythonのmath.log()メソッドを使用する方法と、底の変換公式を使用し、底を10とした場合の2通り計算する。
■今回使用するライブラリ
今回は、math.log()を使用し、常用対数を解く
※math.log()は常用対数以外でも使用可能
▼使い方
# ライブラリのインポート
import math
# 使用方法(例:log底真数)
math.log(真数, 底)■サンプルコード
# -*- Coding:UTF-8 -*-
import math
# 問題1:log10 6
ques1 = math.log(6, 10)
print('問題1:' + str(ques1))
# 問題2:log10 18
ques2 = math.log(18, 10)
print('問題2:' + str(ques2))
# 問題3:log3 8
ques3 = math.log(8, 3)
print('問題3:' + str(ques3))
# 問題3:log3 8 -> 底を10に揃える(底の変換公式)
# -> log10 8 / log10 3
ques3_2 = math.log(8, 10) / math.log(3, 10)
print('問題3(底の変換後):' + str(ques3_2))
■実行結果
問題1:0.7781512503836435
問題2:1.2552725051033058
問題3:1.892789260714372
問題3(底の変換後):1.892789260714372★問題3については常用対数に変換(※底の変換公式を使用)し、log108 / log103にした後に解いた場合と、そのままlog38を解いた場合と同じ結果となる。
※底の変換公式
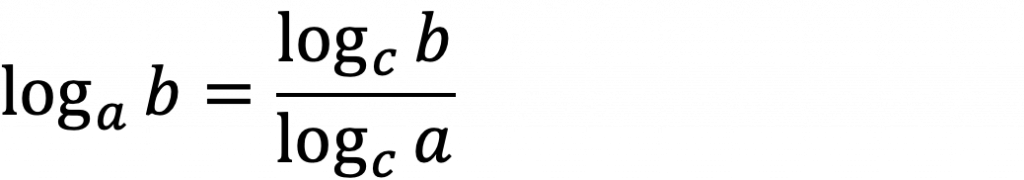
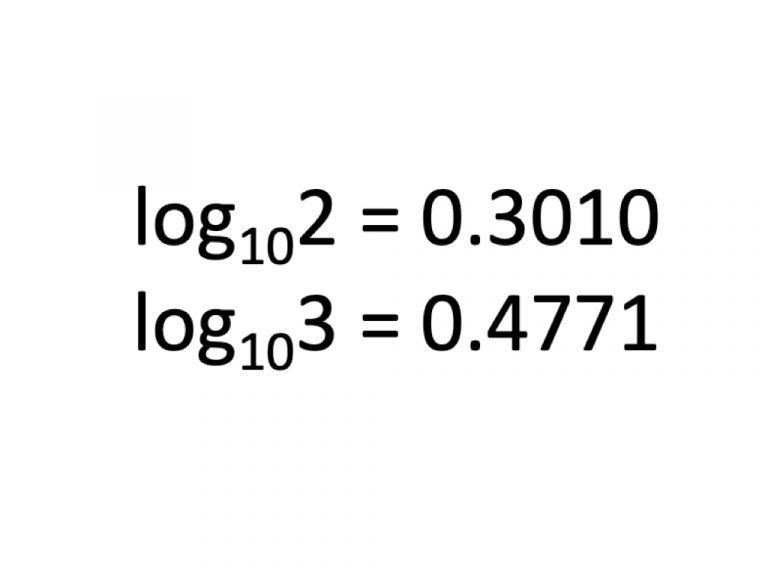

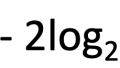

コメント