■対数方程式
対数方程式を解く場合は、まず、真数条件をチェックしてから解答する。
(例)
log4(x + 8) = log2(x + 2)を解く
真数条件:
①x + 8 > 0 かつ ②x + 2 > 0
①x > -8 かつ ②x > -2
よって、①②ともに満たす条件は、x > -2 である(※1)
(※1)イメージ図

log4(x + 8) = log2(x + 2)
log2(x + 8) / log24 = log2(x + 2) ←底の変換公式(※2)で底を2に揃える
log2(x + 8) / log222 = log2(x + 2)
log2(x + 8) / 2log22 = log2(x + 2) ←log22=1
log2(x + 8) / 2 = log2(x + 2)
log2(x + 8) = 2log2(x + 2)
log2(x + 8) = log2(x + 2)2 ←底が2であり、かつ、真数部は等しいので
(x + 8) = (x + 2)2
(x + 8) = x2 + 4x + 4
x2 + 3x – 4 = 0
(x – 1)(x + 4) = 0
x > -2 より、x = 1
(※2 底の変換公式)
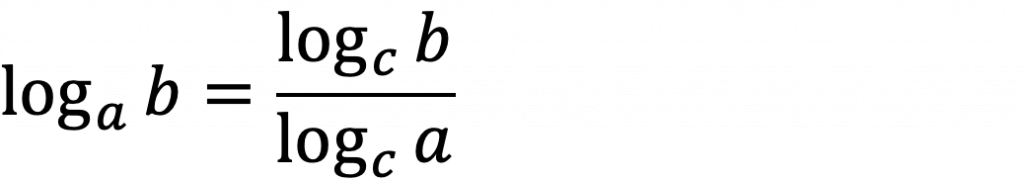
■sympy.log()を使用して対数(log)を表現する
sympy.log()を使用して対数を解く場合、
sympy.log(真数, 底)と表記する。
すなわち、log24 をsympy.log()を使用して解く場合は、
import sympy
ans = sympy.log(4, 2)
print(ans) # 答えは2と表記する。
■例題
▼問題1
log3x – log3(4 – x) = 0
▼問題2
log4(x + 8) – log2(x + 2) = 0
▼問題3
log6(x – 2) + log6(x + 3) – 1 = 0
▼問題4
(log2x)2 – 2log2x – 3 = 0
■サンプルコード
# -*- Coding:UTF-8 -*-
import sympy
# 文字列をセット
x = sympy.Symbol('x')
# 問題1
ans1 = sympy.solve(sympy.log(x, 3) - sympy.log(4 - x, 3), x)
# 問題2
ans2 = sympy.solve(sympy.log(x + 8, 4) - sympy.log(x + 2, 2), x)
# 問題3
ans3 = sympy.solve(sympy.log(x - 2, 6) + sympy.log(x + 3, 6) - 1, x)
# 問題4
ans4 = sympy.solve(sympy.log(x, 2) ** 2 - 2 * sympy.log(x, 2) - 3, x)
print('問題1:x = ' + str(ans1))
print('問題2:x = ' + str(ans2))
print('問題3:x = ' + str(ans3))
print('問題4:x = ' + str(ans4))
■実行結果
問題1:x = [2]
問題2:x = [1]
問題3:x = [3]
問題4:x = [1/2, 8]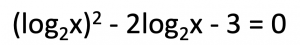
コメント