■度数法と弧度法
▼度数法
円1周の角度を360度(°)で表す方法
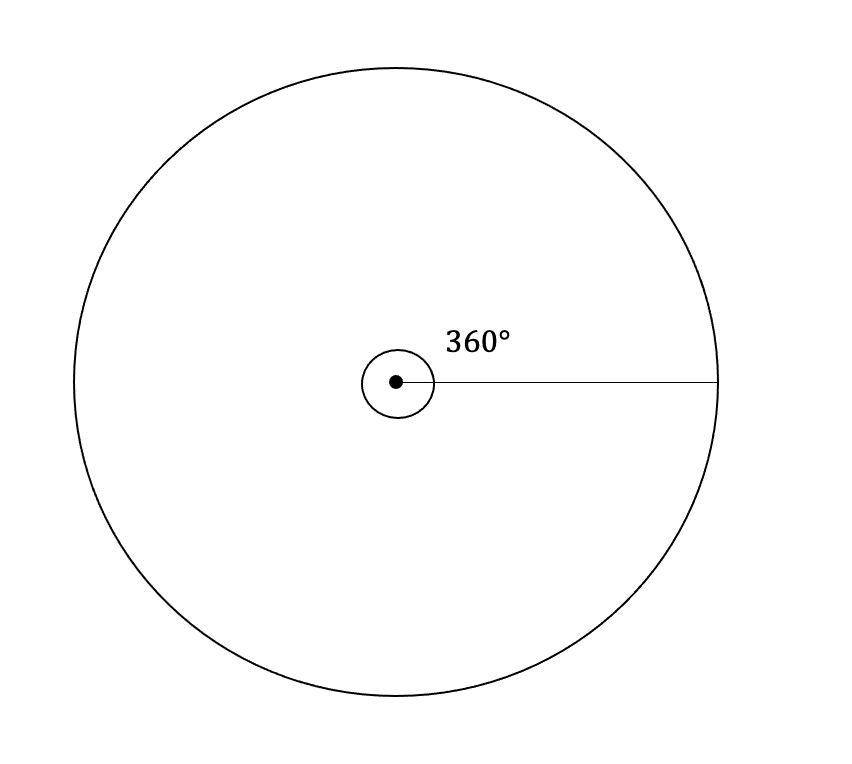
▼弧度法
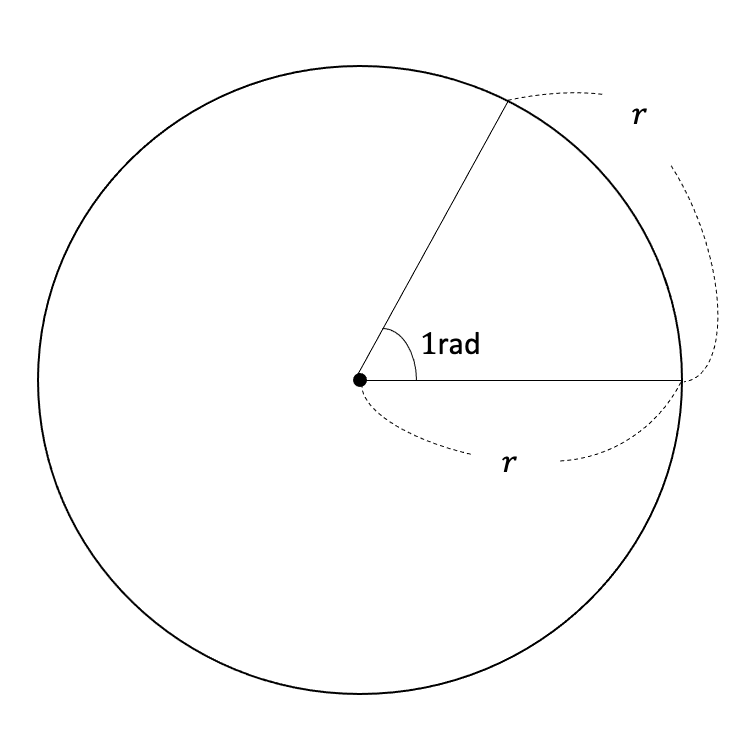
半径に等しい弧の長さに対する中心角の大きさを1rad(ラジアン)と表す。
一般的に角度180° = πラジアンと表記する。
※π = 3.141592・・・
■例題
以下の問題について、
度数法の値は弧度法
弧度法の値は度数法
に変換する。
なお、πの値については、pythonのmath.pi()を使用するものとする。
問題1:30°を弧度法で表記
問題2:120°を弧度法で表記
問題3:360°を弧度法で表記
問題4:(3/4)πを度数法で表記
問題5:(5/3)πを度数法で表記
問題6:(5/12)πを度数法で表記
■サンプルコード
# -*- Cording:UTF-8 -*-
import math
# [事前準備]πの値を変数に格納(弧度法->度数法変換用)
pi = math.pi
# 問題1:30°を弧度法で表記
q1 = 30
ans1 = math.radians(q1)
print('問題1:30° -> ', ans1)
# 問題2:120°を弧度法で表記
q2 = 120
ans2 = math.radians(q2)
print('問題2:120° -> ', ans2)
# 問題3:360°を弧度法で表記
q3 = 360
ans3 = math.radians(q3)
print('問題3:360° -> ', ans3)
# 問題4:(3/4)πを度数法で表記
q4 = (3 / 4) * pi
ans4 = math.degrees(q4)
print('問題4:(3/4)π -> ', ans4)
# 問題5:(5/3)πを度数法で表記
q5 = (5 / 3) * pi
ans5 = math.degrees(q5)
print('問題5:(5/3)π -> ', ans5)
# 問題6:(5/12)πを度数法で表記
q6 = (5 / 12) * pi
ans6 = math.degrees(q6)
print('問題6:(5/12)π -> ', ans6)
■実行結果
問題1:30° -> 0.5235987755982988
問題2:120° -> 2.0943951023931953
問題3:360° -> 6.283185307179586
問題4:(3/4)π -> 135.0
問題5:(5/3)π -> 300.0
問題6:(5/12)π -> 75.0


コメント