■正弦(sin)のグラフと余弦(cos)のグラフ
▼正弦(sin)のグラフ:y = sinθ
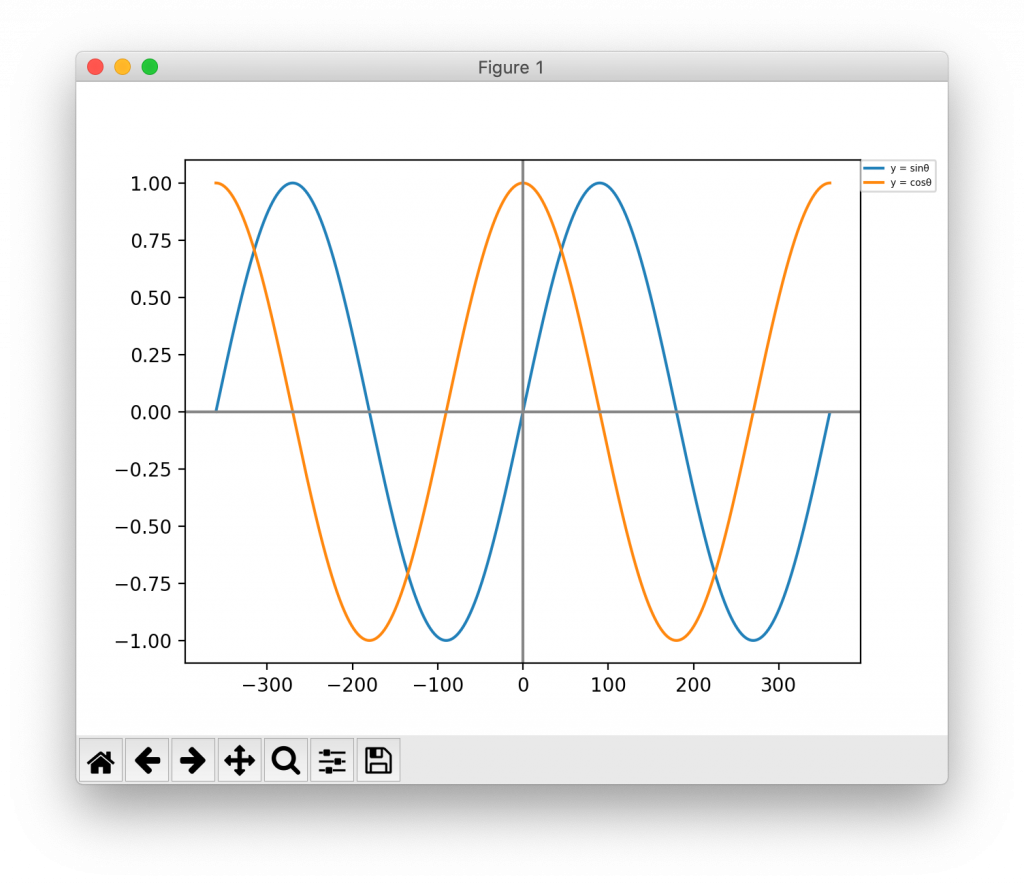
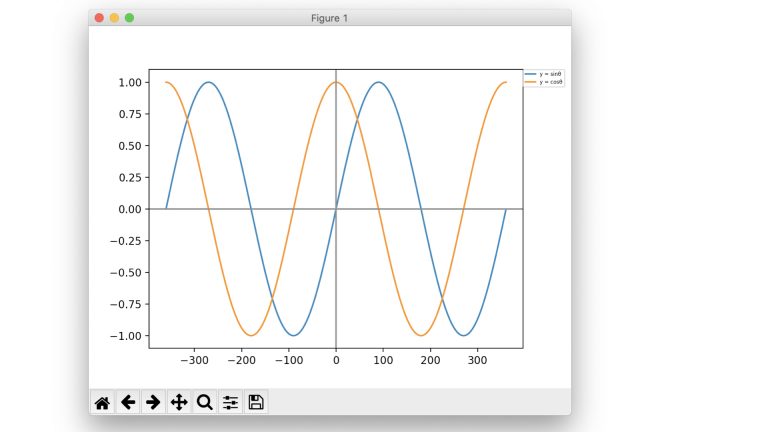
正弦(sin)のグラフは単位円の高さ(y座標)の変化に着目する。(図1:青色部分)

▼余弦(cos)のグラフ:y = cosθ
正弦(cos)のグラフは単位円におけるx軸上の底辺の変化に着目する。(図2:オレンジ部分)

※y = tanθは「θ=90°」をとれないため今回のグラフは割愛する。
■サンプルコード
# -*- Coding:UTF-8 -*-
import math
import numpy as np
from numpy.linalg import solve
from matplotlib import pyplot as plt
# グラフを作成する関数
def MakeGraph():
# 角度(θ)の値を便宜上、-360°〜360°にする(0.1°間隔で配列に格納)
thetamin = -360
thetamax = 360
thetainterval = 0.1
theta = np.arange(thetamin, thetamax, thetainterval)
# sinθを格納する配列
ysin = []
# cosθを格納する配列
ycos = []
# 角度(θ)の配列分ループ処理
for i in range(len(theta)):
# 度数法→ラジアンに変換
radian_theta = math.radians(theta[i])
# y = sinθの値を格納
ysin.append(math.sin(radian_theta))
# y = cosθの値を格納
ycos.append(math.cos(radian_theta))
# グラフを作成
plt.plot(theta, ysin, label = "y = sinθ")
plt.plot(theta, ycos, label = "y = cosθ")
# ラベルの表示
plt.legend(bbox_to_anchor=(1, 1), loc='upper left', borderaxespad=0, fontsize=5)
########## グラフにθ(x)軸,y軸(0)を図示 ##########
# 補助線(0)を作成 [axhline:水平 axvline:垂直]
plt.axhline(y = 0, color = "gray")
plt.axvline(x = 0, color = "gray")
############################################
# グラフを表示
plt.show()
# メイン処理
if __name__ == '__main__':
# グラフの作成
MakeGraph()
■実行結果
コメント