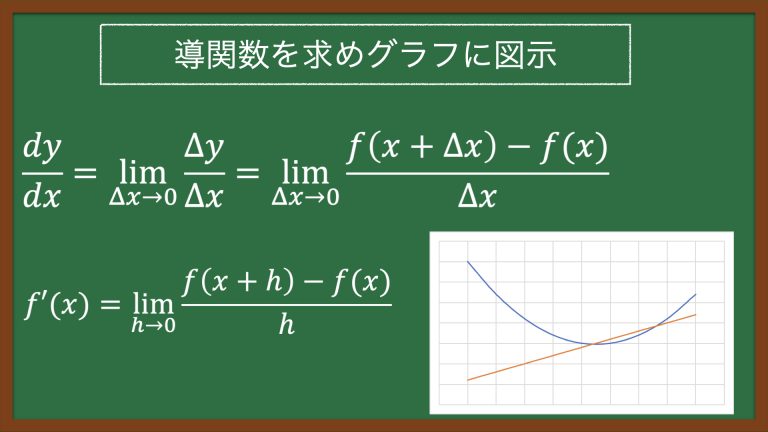
■導関数
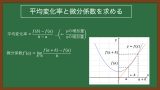
ある関数f(x)について、任意の点(a, f(a))における微分係数(傾き)を求める方法は、以下の参考ページで行なったが、毎回、特定の点ごとに微分係数を求めるのは大変である。
そこで、ある関数f(x)における、すべてのxについて微分可能であるとした時、すべてのxに対応したf'(x)を求めれば、容易に微分係数が求められる。
このf'(x)を関数f(x)の導関数という。
▼導関数の公式
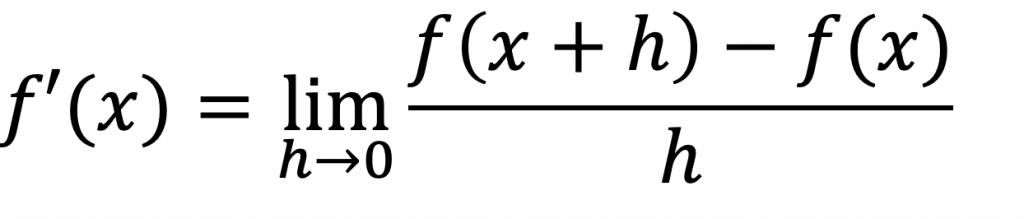
他にも導関数は、以下のように表記される。
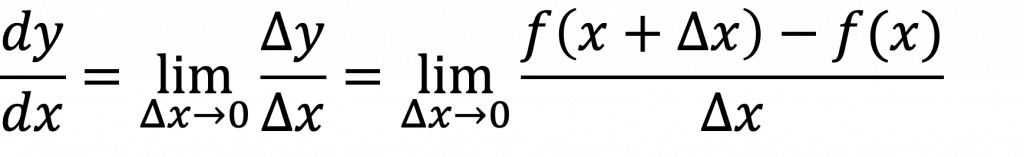
▼参考ページ
■例題
(1)関数f(x) = x2 + x について、導関数f'(x)を求める。
(2)関数f(x)および導関数f'(x)をグラフに図示する。
(1)関数f(x) = x2 + x について、導関数f'(x)を求める。
pythonで極限(lim)の計算を行うときは、sympyライブラリのlimit()を使用する。
▼sympy.limit()の使い方
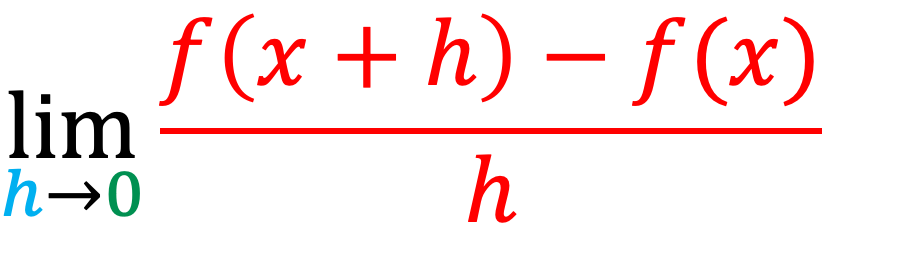
上記計算式の場合、設定する引数は以下の通り。
sympy.limit((f(x + h) – f(x)) / h , h, 0)
▼サンプルコード
# -*- Coding:UTF-8 -*-
import sympy
# 関数:f(x) = x**2 + x
def f(x):
y = x**2 + x
return y
# 文字列をセット
h = sympy.Symbol('h')
x = sympy.Symbol('x')
# 導関数を求める
result = sympy.limit((f(x+h)-f(x))/h, h, 0)
print(f(x), 'の導関数は', result)▼実行結果
x**2 + x の導関数は 2*x + 1(2)関数f(x)および導関数f'(x)をグラフに図示する。
関数f(x) = x2 + x および(1)で算出した導関数f'(x) = 2x + 1を使用して、グラフを図示する。
なお、便宜上、xは-5から5までの範囲とする。
▼サンプルコード
# -*- Coding:UTF-8 -*-
import numpy as np
from matplotlib import pyplot as plt
# 関数:f(x) = x**2 + x
def f(x):
y = x**2 + x
return y
# 導関数:f'(x) = 2x + 1
def f_d(x):
y = 2 * x + 1
return y
# グラフ作成
# 便宜上、-5から5までの値を0.1間隔で設定
x_min = -5
x_max = 5
x_interval = 0.1
x = np.arange(x_min, x_max, x_interval)
# 関数f(x)を格納する配列
y1 = []
# 導関数f'(x)を格納する配列
y2 = []
# それぞれ配列に格納していく(便宜上、nは0.1間隔でセット)
for i in range(len(x)):
y1.append(f(x[i]))
y2.append(f_d(x[i]))
# 関数f(x)のグラフを作成
plt.plot(x, y1)
# 導関数f'(x)のグラフを作成
plt.plot(x, y2)
# グラフにx軸,y軸(0)を図示
# 補助線(0)を作成 [axhline:水平 axvline:垂直]
plt.axhline(y=0, color="gray")
plt.axvline(x=0, color="gray")
# グラフを表示
plt.show()
▼実行結果
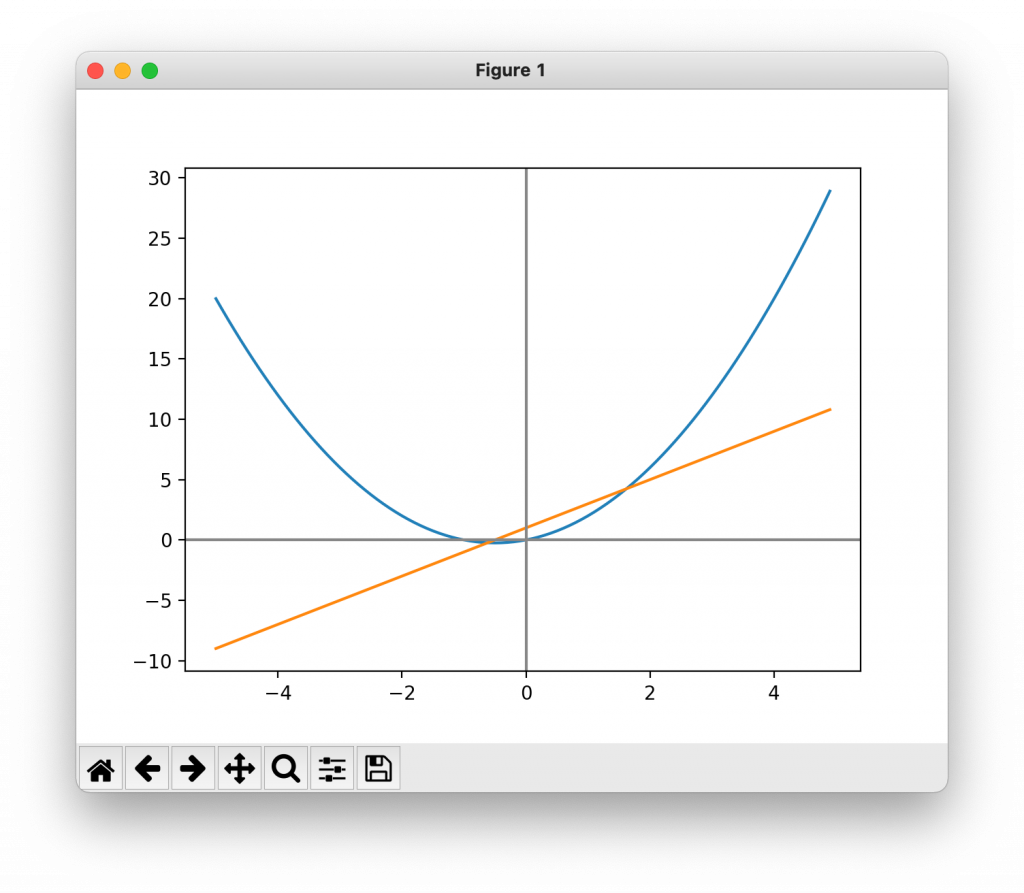
コメント
[…] 【Python】微分:導関数を求めグラフに図示■導関数ある関数f(x)について、任意の点(a, f(a))における微分係数(傾き)を求める方法は、以下の参考ページで行なったが、毎回、特定の […]