■速度の合成
任意の速度で動いている物体(電車、風、川など)の中で動いている物体(人、飛行機、船など)に対して、速度を合成することができる。
また、速度の合成については、以下の公式で求めることができる。
・「速度の合成」の公式
地面に対して、速度V1で動いている物体の中で、速度V2で動いている物体の地面に対する速度Vは、 V = V1 + V2
▼例題1
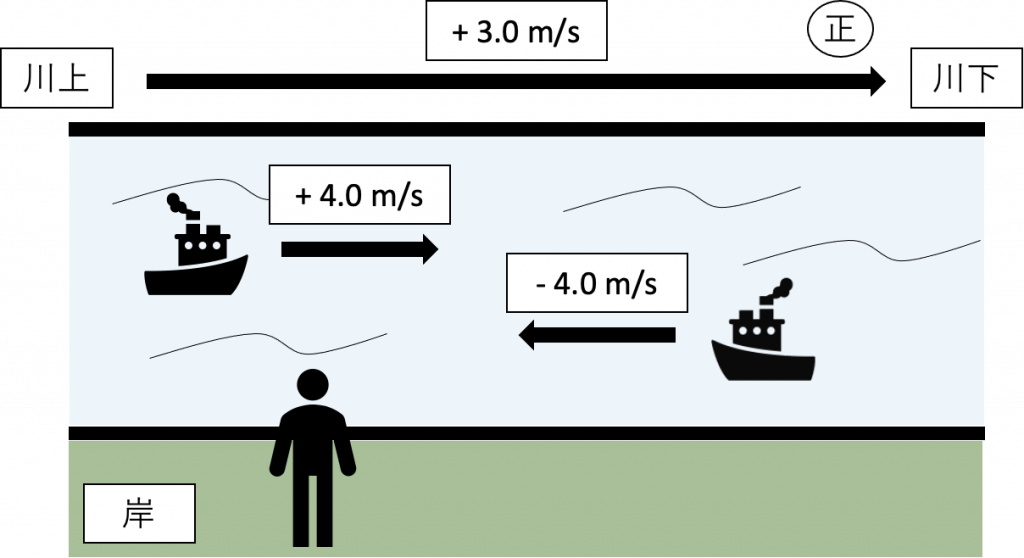
速度3.0 m/s で流れる川に速度4.0 m/s でボートが進む時、以下の2問をPythonを使用して解く。
なお、川上から川下への方向を正とし、川下から川上の方向を負とする。
問1:川下に向かって進む時、岸から見たボートの速度を求める。
問2:川上に向かって進む時、岸から見たボートの速度を求める。
▼サンプルコード
例題1のサンプルコードを以下に示す。
# 川の速度(川上→川下):3.0 m/s
river_v = 3.0
# ボートの速度(川上→川下):4.0 m/s
boat1_v = 4.0
# ボートの速度(川上←川下):-4.0 m/s
boat2_v = -4.0
# 問1:川の方向にボートを漕ぐ
print(river_v + boat1_v, 'm/s')
# 問2:川と逆方向にボートを漕ぐ
print(river_v + boat2_v, 'm/s')▼実行結果
例題1の「▼サンプルコード」について、実行結果を以下に示す。
7.0 m/s
-1.0 m/s川の流れと同じ方向(川上→川下)に進む船の速度は、合算して7.0 m/s進む。
川の流れと逆の方向(川上←川下)に進む船の速度は、合算して-1.0 m/s進む(川上に1.0m/s進む)。
■相対速度
自分が歩きで相手が走っている場合は、簡単に抜かれ、差が開いていく一方で、自分も相手も走っていれば、あまり差が開かない。
このような、自分の速度に対して、相手の見かけの速度を相対速度という。
相対速度は、以下の公式で求めることができる。
任意の物体の速度V1に対する、任意の物体の見かけの速度をV2とした時の相対速度Vは、 V = V2 - V1
▼例題2
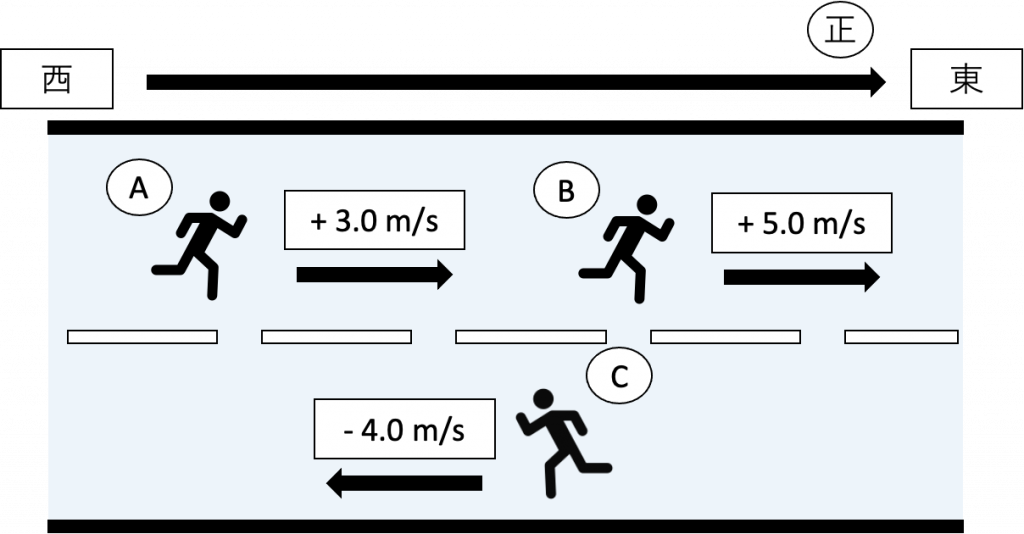
A君が西→東の方向へ3.0 m/sの速度で走っているとき、B君は西→東へ5.0 m/s、C君は東→西へ4.0 m/sの速度で走っている。
このときの以下の問についてPythonを使用して解く。
なお、西→東の方向を正とし、西←東の方向を負とする。
問1:A君から見たB君の速度を求める。
問2:B君から見たA君の速度を求める。
問3:A君から見たC君の速度を求める。
▼サンプルコード
例題2のサンプルコードを以下に示す。
# Aの速度(西→東):3.0 m/s
A_v = 3.0
# Bの速度(西→東):5.0 m/s
B_v = 5.0
# Cの速度(西←東):-4.0 m/s
C_v = -4.0
# 問1:Aから見たBの速度
print(B_v - A_v, 'm/s')
# 問2:Bから見たAの速度
print(A_v - B_v, 'm/s')
# 問3:Aから見たCの速度
print(C_v - A_v, 'm/s')▼実行結果
例題2の「▼サンプルコード」について、実行結果を以下に示す。
2.0 m/s
-2.0 m/s
-7.0 m/sA君・B君ともに西→東へ進んでおり、B君の方が 2.0m/s速く進んでいる。
すなわち、A君から見るB君の速度は、+2.0 m/sとなり、B君から見るA君の速度は-2.0 m/sとなる。
※B君からA君を見ると、東→西へ進んでいるように見える。
A君は西→東の方向へ進んでいるのに対して、C君は東→西の方向へ進んでいるので、A君とC君との距離は縮まり、その後離れていくため、お互いに逆方向へ進む分見かけの速度は速くなる。

コメント