■概要
プログラムの処理を実装する上で、処理時間は非常に重要な評価の一つである。
本稿では、配列に格納した、1からN番目までの数字から任意の数字について、全探索と2分探索で検索を行い、検索回数と処理時間を比較する。
なお、検索処理時間を公平にするため、検索値は、最後の数値(N番目の数字)とする。
また、Nの値が大きくになるにつれて、処理時間がどのように増加していくか判定するために、
Nの値(最大値)を
「1」、「10」、「100」、「1000」、「10000」、「100000」、「1000000」、「10000000」、「100000000」とする。
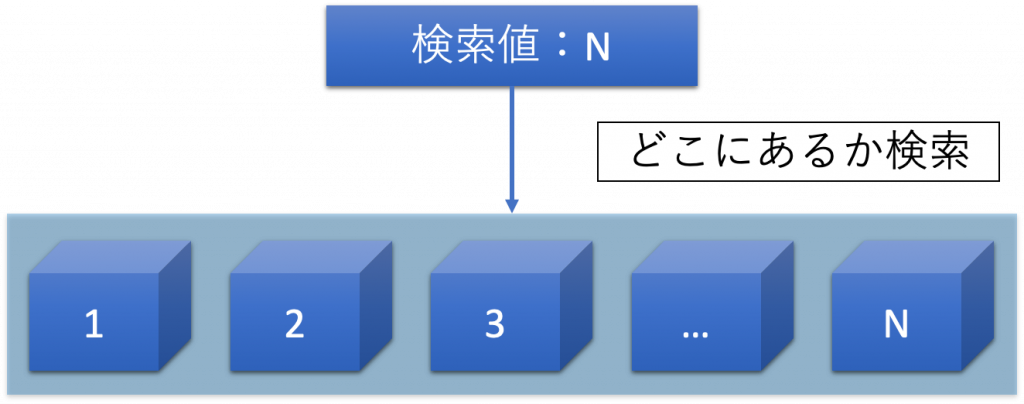
■全探索
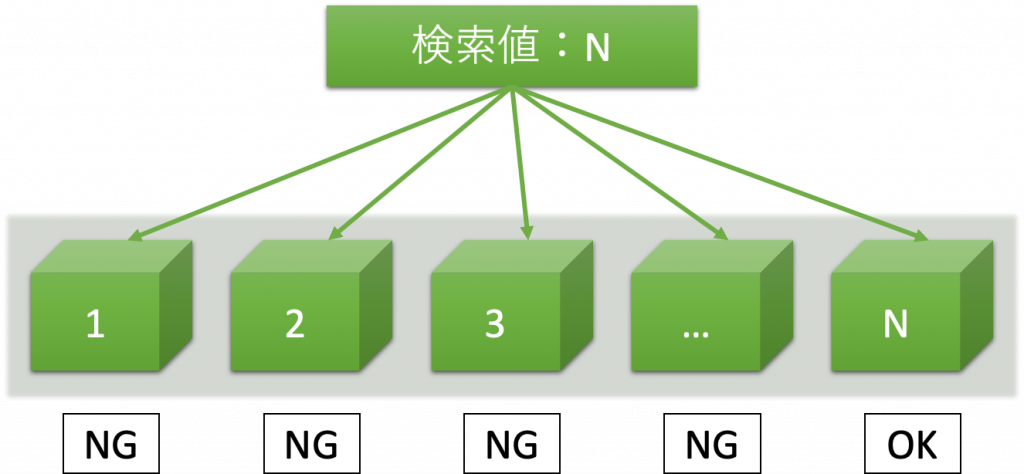
あり得るすべてのパターンを調べる方法を全探索という。
全探索は非常にシンプルなアルゴリズムではあり、まず、全探索で実装し、処理時間がどのくらいか計測し、現実的な時間かどうか評価し、非現実的であれば、処理の変更を行う。
▼フローチャート
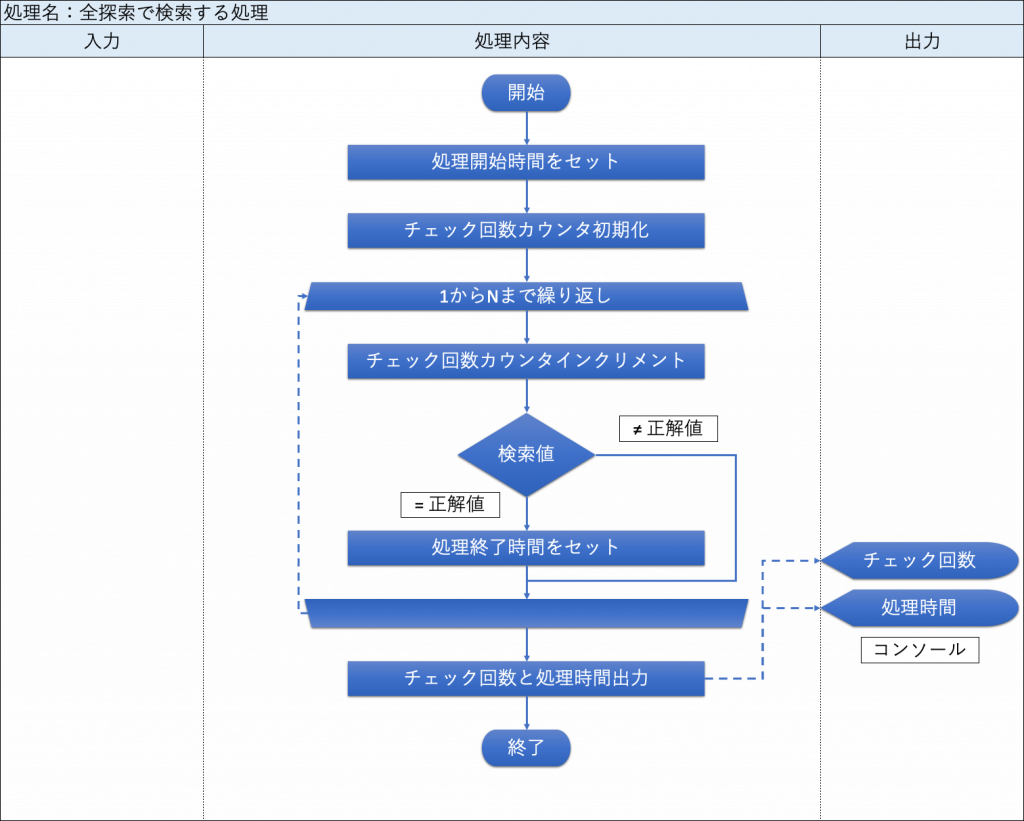
・全探索で検索する処理
「全探索で検索する処理」のフローチャートを、下図に示す。
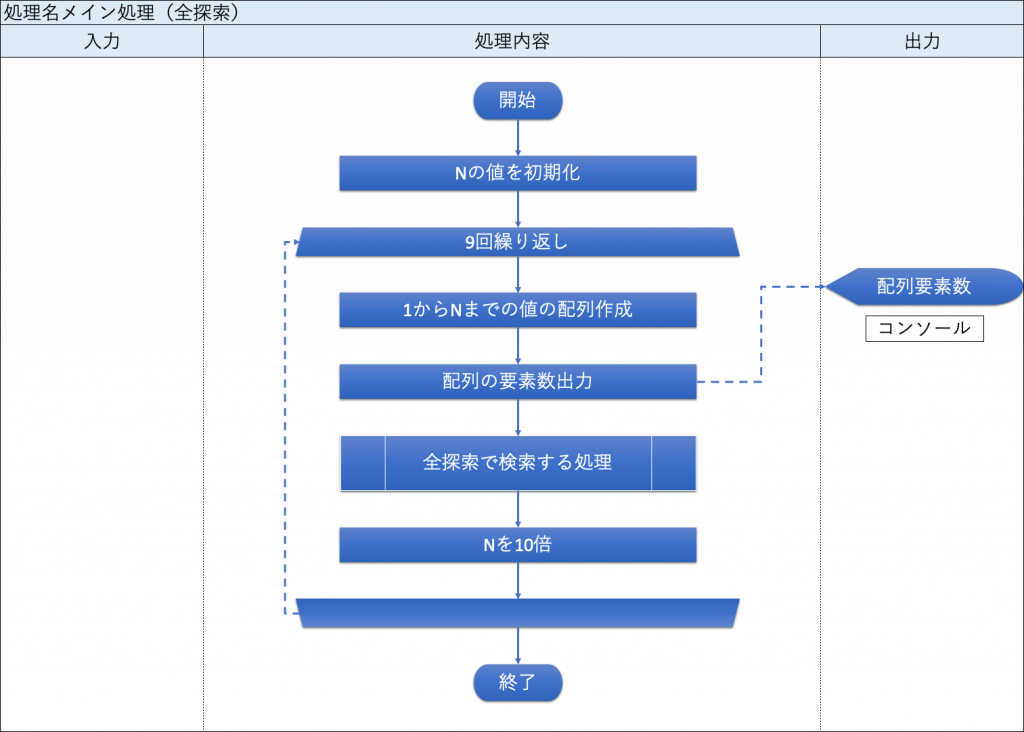
・メイン処理(全探索)
全探索における「メイン処理」のフローチャートを、下図に示す。
▼プログラム仕様
・全探索で検索する処理
「全探索で検索する処理」について、<引数と戻り値>および<処理内容>を下表に示す。
<引数と戻り値>
| 項目 | 型 | 項目内容 |
|---|---|---|
| 第1引数 | list型 ※データ:int型 | 1からNまでの数値を格納した配列 |
| 第2引数 | int型 | 正解値 |
| 戻り値 | – | なし |
<処理内容>
| 入力 | 処理内容 | 出力 |
|---|---|---|
| – | 処理開始時間をセットする。 | – |
| – | チェック回数カウント初期化する。 初期値:0 | – |
| – | ■ループ処理:1からNまで繰り返し |チェック回数カウンタをインクリメントする。 |▼条件分岐:検索値 = 正解値 ||処理終了時間をセットする。 |▲ ■ | – |
| – | チェック回数と処理時間(※)を出力する。 (※)秒:処理終了時間ー処理開始時間 | 【コンソール】 チェック回数 処理時間 |
・メイン処理(全探索)
全探索における「メイン処理」について、<引数と戻り値>および<処理内容>を下表に示す。
<引数と戻り値>
| 項目 | 型 | 項目内容 |
|---|---|---|
| 第1引数 | – | なし |
| 戻り値 | – | なし |
<処理内容>
| 入力 | 処理内容 | 出力 |
|---|---|---|
| – | Nの値について、初期値をセットする。 初期値:1 | – |
| – | ■ループ処理:9回繰り返し |1からNまでの値を配列に格納する。 |配列の要素数を出力する。 |「全探索で検索する処理」呼び出し。 |Nの値を10倍する。 ■ | 【コンソール】 配列の要素数 |
▼サンプルコード
import time
# 全探索で検索する処理
def FullSearch(list_value, ans_num):
# 処理開始時間をセット
start_time = time.time()
# チェック回数カウント初期化
count = 0
# 配列の要素数分繰り返し
for i in range(len(list_value)):
# チェック回数インクリメント
count = count + 1
# 正解の場合
if (list_value[i] == ans_num):
# 処理終了時間をセット
end_time = time.time()
break
# チェック回数と処理時間を出力
print('チェック回数:', count)
print('処理時間:', round(end_time - start_time, 2))
# メイン処理
if __name__ == '__main__':
# 配列要素の初期値セット
n = 1
# 9回繰り返し
for _ in range(9):
# 1からnまでの値を配列に格納
num_list = list(range(1, n+1))
# 配列要素数を出力
print('n = ', n)
# 全探索で検索
FullSearch(num_list, n)
# 2分探索で検索
# BinarySearch(num_list, n)
# 区切りを出力
print('********************')
# 配列要素数を10倍
n = n * 10
▼実行結果
n = 1
チェック回数: 1
処理時間: 0.0
********************
n = 10
チェック回数: 10
処理時間: 0.0
********************
n = 100
チェック回数: 100
処理時間: 0.0
********************
n = 1000
チェック回数: 1000
処理時間: 0.0
********************
n = 10000
チェック回数: 10000
処理時間: 0.0
********************
n = 100000
チェック回数: 100000
処理時間: 0.01
********************
n = 1000000
チェック回数: 1000000
処理時間: 0.12
********************
n = 10000000
チェック回数: 10000000
処理時間: 0.87
********************
n = 100000000
チェック回数: 100000000
処理時間: 17.92
********************■2分探索
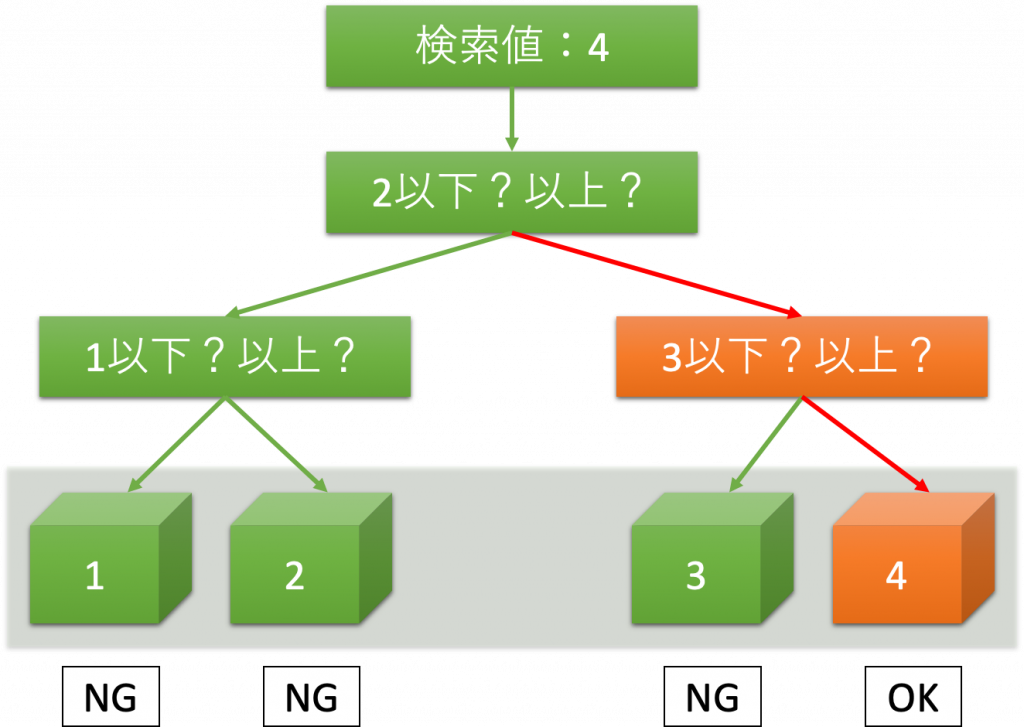
下図のように、全量の半分に対して、「以上」か「以下」の判別を繰り返し、検索値を調べていく方法を2分探索という。
2分探索は、全探索(※)とは異なり、検索値に関わらず、判別回数が変動しないのが特徴である。
(※)全探索の場合、例えば「1〜8」の値に対し、1から順番に昇順で検索していくと、
検索値が「1」の場合は、1回で検索が終わるが、
検索値が「8」の場合は、8回検索する必要がある。
▼フローチャート
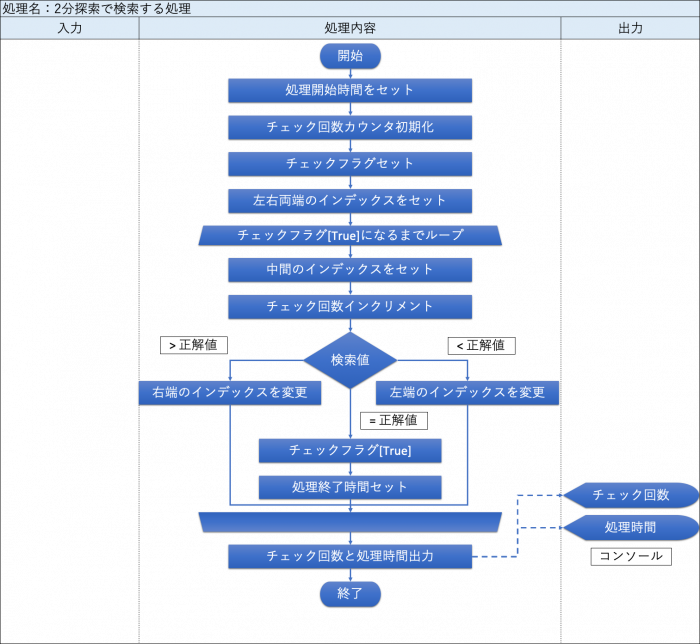
・2分探索で検索する処理
「2分探索で検索する処理」のフローチャートを、下図に示す。
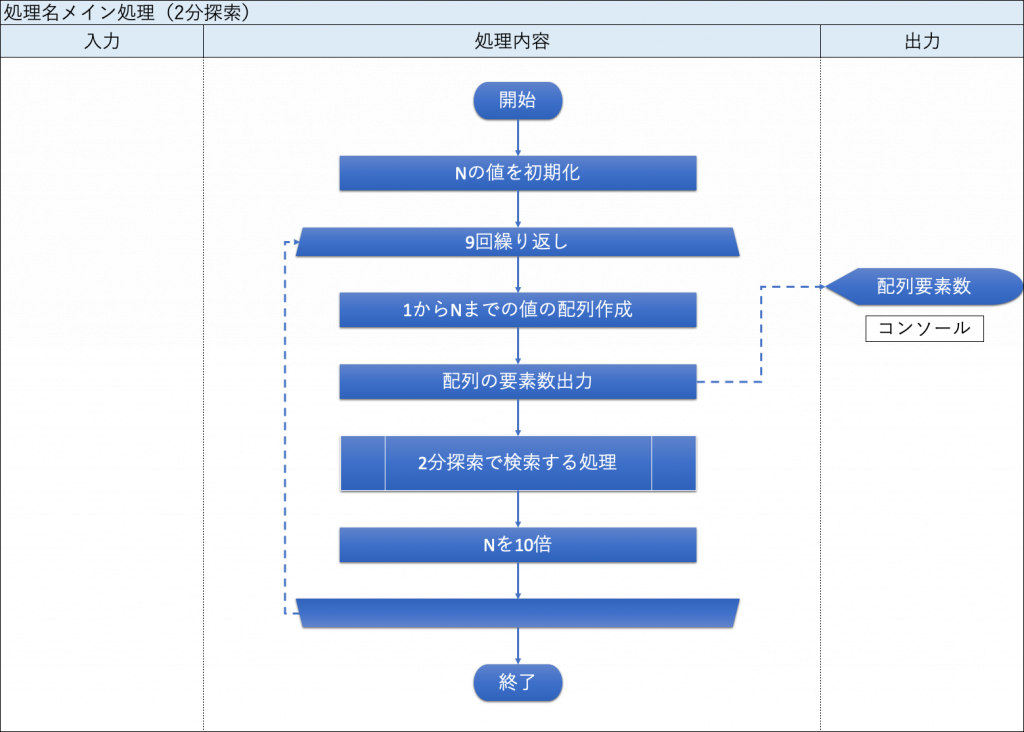
・メイン処理(2分探索)
2分探索における「メイン処理」のフローチャートを、下図に示す。
▼プログラム仕様
・2分探索で検索する処理
「2分探索で検索する処理」について、<引数と戻り値>および<処理内容>を下表に示す。
<引数と戻り値>
| 項目 | 型 | 項目内容 |
|---|---|---|
| 第1引数 | list型 ※データ:int型 | 1からNまでの数値を格納した配列 |
| 第2引数 | int型 | 正解値 |
| 戻り値 | – | なし |
<処理内容>
| 入力 | 処理内容 | 出力 |
|---|---|---|
| – | 処理開始時間をセットする。 | – |
| – | チェック回数カウント初期化する。 初期値:0 | – |
| – | チェックフラグをセットする。 初期値:False | – |
| – | 左右両端のインデックスの初期値をセットする。 初期値: ・左端:0 ・右端:配列の要素数 | – |
| – | ■ループ処理:チェックフラグが[True]になるまで |中間のインデックス番号をセットする。 |(左端+右端のインデックス)/ 2 ※少数切り捨て |チェック回数カウンタをインクリメントする。 |▼条件分岐 |【検索値 > 正解値の場合】 ||右端のインデックスを変更する。 ||(中間のインデックス – 1) |------ |【検索値 < 正解値の場合】 ||左端のインデックスを変更する。 ||(中間のインデックス + 1) |------ |【検索値 = 正解値の場合】 ||チェックフラグを[True]に変更する。 ||処理終了時間をセットする。 |▲ ■ | – |
| – | チェック回数と処理時間(※)を出力する。 (※)秒:処理終了時間ー処理開始時間 | 【コンソール】 チェック回数 処理時間 |
・メイン処理(2分探索)
2分探索における「メイン処理」について、<引数と戻り値>および<処理内容>を下表に示す。
<引数と戻り値>
| 項目 | 型 | 項目内容 |
|---|---|---|
| 第1引数 | – | なし |
| 戻り値 | – | なし |
<処理内容>
| 入力 | 処理内容 | 出力 |
|---|---|---|
| – | Nの値について、初期値をセットする。 初期値:1 | – |
| – | ■ループ処理:9回繰り返し |1からNまでの値を配列に格納する。 |配列の要素数を出力する。 |「2分探索で検索する処理」呼び出し。 |Nの値を10倍する。 ■ | 【コンソール】 配列の要素数 |
▼サンプルコード
import time
# 二分探索で検索する処理
def BinarySearch(list_value, ans_num):
# 処理開始時間をセット
start_time = time.time()
# チェック回数カウント初期化
count = 0
# チェックフラグセット
chk_flg = False
# 左右両端のインデックスをセット
left_index = 0
right_index = len(list_value)
# チェックフラグが[True]になるまで繰り返し
while not chk_flg:
# 中間のインデックス番号をセット(少数切り捨て)
middle_index = (left_index + right_index) // 2
# チェック回数インクリメント
count = count + 1
# 検索値 > 正解値
if (list_value[middle_index] > ans_num):
# 右端のインデックスを変更
right_index = middle_index - 1
# 検索値 < 正解値
elif (list_value[middle_index] < ans_num):
# 左端のインデックスを変更
left_index = middle_index + 1
# 検索値 = 正解値
elif (list_value[middle_index] == ans_num):
# チェックフラグを[True]
chk_flg = True
# 処理終了時間をセット
end_time = time.time()
# チェック回数と処理時間を出力
print('チェック回数:', count)
print('処理時間:', round(end_time - start_time, 2))
# メイン処理
if __name__ == '__main__':
# 配列要素の初期値セット
n = 1
# 9回繰り返し
for _ in range(9):
# 1からnまでの値を配列に格納
num_list = list(range(1, n+1))
# 配列要素数を出力
print('n = ', n)
# 2分探索で検索
BinarySearch(num_list, n)
# 区切りを出力
print('********************')
# 配列要素数を10倍
n = n * 10
▼実行結果
n = 1
チェック回数: 1
処理時間: 0.0
********************
n = 10
チェック回数: 3
処理時間: 0.0
********************
n = 100
チェック回数: 6
処理時間: 0.0
********************
n = 1000
チェック回数: 9
処理時間: 0.0
********************
n = 10000
チェック回数: 13
処理時間: 0.0
********************
n = 100000
チェック回数: 16
処理時間: 0.0
********************
n = 1000000
チェック回数: 19
処理時間: 0.0
********************
n = 10000000
チェック回数: 23
処理時間: 0.0
********************
n = 100000000
チェック回数: 26
処理時間: 0.0
********************■全探索と2分探索の比較
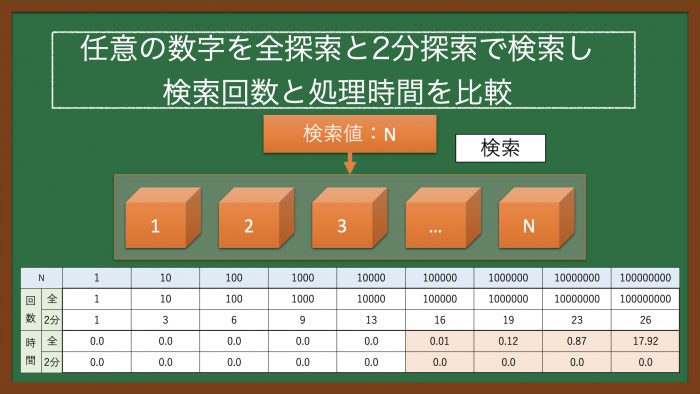
前項「■全探索」と「■2分探索」の処理回数および処理時間(秒)を下表に示す。

「全探索」と「2分探索」の処理回数を比較すると、「2分探索」の方が明らかに回数が少ないことがわかる。
また、処理時間についても、「全探索」の方が最大約18秒かかることから、処理性能に違いが生じていることがわかる。
※処理時間の「0.0」は「0.0秒未満」であることを示す。

コメント