■2次方程式における解の公式
2次方程式:
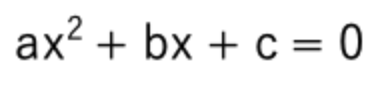
の場合、xの解は以下の公式で解くことができる。
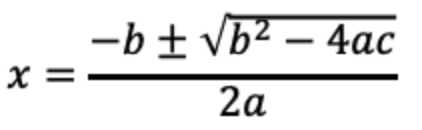
■例題
二次方程式、ax2 + bx + c = 0 について、a, b, cの値が以下の場合、xの値を解の公式を使用して解く。
①a = 1、b = 3、c = 2
②a = 6、b = -18、c = -60
③a = -2、b = 2、c = -6
■実装概要
▼実装概要(2次方程式:解の公式関数)
引数:a, b, c
戻り値:x(配列)
①戻り値用配列xをセットする。(※ 解の公式は2つの解が発生するため)
②解の公式1の結果を戻り値用配列xに追加する。
③解の公式2の結果を戻り値用配列xに追加する。
④戻り値用配列xを返す。
■サンプルコード
# -*- Coding: UTF-8 -*-
import math
# 2次方程式:解の公式関数
# 引数 :a, b, c
# 戻り値 :x(解の公式の処理結果(配列))
def Solution(a, b, c) -> list:
x = []
x1 = (-b + math.sqrt(b ** 2 - 4 * a * c)) / (2 * a)
x.append(x1)
x2 = (-b - math.sqrt(b ** 2 - 4 * a * c)) / (2 * a)
x.append(x2)
# xの解を返す。
return x
# メイン処理
if __name__ == '__main__':
# 例題①
a = 1
b = 3
c = 2
# 2次方程式:解の公式関数を呼び出し、結果を表示する。
print('x = ', Solution(a, b, c))
# 例題②
a = 6
b = -18
c = -60
# 2次方程式:解の公式関数を呼び出し、結果を表示する。
print('x = ', Solution(a, b, c))
# 例題③
a = 2
b = -16
c = 30
# 2次方程式:解の公式関数を呼び出し、結果を表示する。
print('x = ', Solution(a, b, c))
■実行結果
x = [-1.0, -2.0]
x = [5.0, -2.0]
x = [5.0, 3.0]
コメント