【Python】ヘロンの公式を使って三角形の面積を求める

■ヘロンの公式

三角形ABCについて、3辺の長さがわかれば、以下のように面積（S）を算出できる。

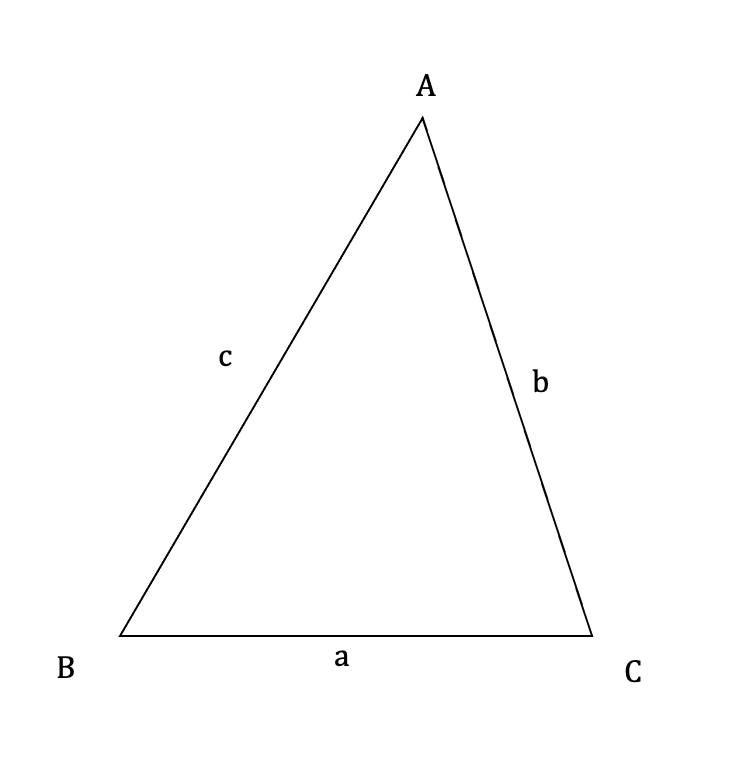
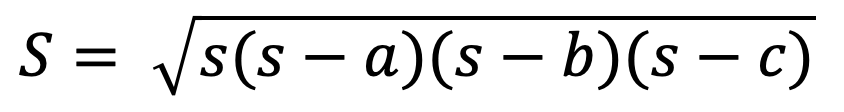
ただし、s（ルート内の小文字 [s]）は以下の通りである

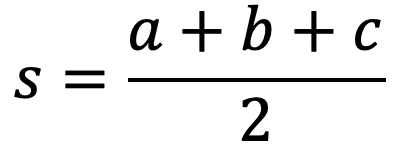
■例題1

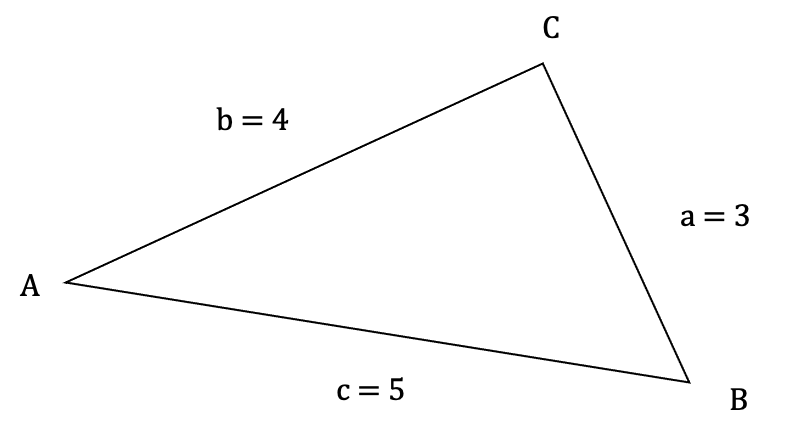
三角形ABCの3辺がそれぞれ a = 3, b = 4, c = 5 の時、
三角形ABCの面積を求める。

▼サンプルコード

# -*- Coding:UTF-8 -*-
import math

# ヘロンの公式関数
def HeronFormula(a: int, b: int, c: int):
    # スモールsの値を算出
    s = (a + b + c) / 2
    # 三角形の面積を算出
    S = math.sqrt(s * (s - a) * (s - b) * (s - c))

    # 面積を戻り値として返す
    return S

# メイン処理
if __name__ == '__main__':

    # 三角形ABCの3辺がそれぞれ a = 3, b = 4, c = 5 の時、
    # 三角形ABCの面積を求める。
    a = 3
    b = 4
    c = 5

    print('三角形の面積：', HeronFormula(a, b, c))

▼実行結果

三角形の面積： 6.0

■例題2

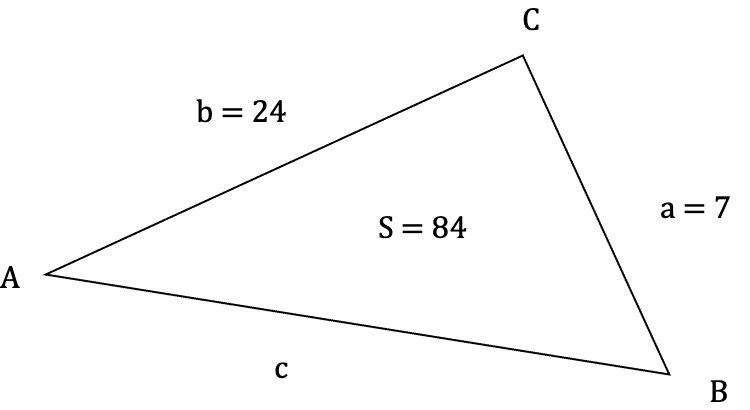
三角形ABCの辺 a = 7、b = 24、面積S = 84の時、
三角形ABCの辺cを求める。

▼サンプルコード

# -*- Coding:UTF-8 -*-
import math
import sympy

# ヘロンの公式を使って辺の長さを求める関数
def HeronToLine(a: int, b: int, S: int):
    # 戻り値用配列をセット
    ans = []

    # 文字列をセット
    c = sympy.Symbol('c')

    # スモールsの値を算出(文字cはそのまま)
    s = (a + b + c) / 2

    # ヘロンの公式を元に辺cについて解く
    # S = √s(s-a)(s-b)(s-c)
    # S**2 = s(s-a)(s-b)(s-c) ：ルートを外すために両辺を2乗
    # s(s-a)(s-b)(s-c) - (S**2) = 0 ：sympy.solove()で使用する形に変形
    tmp = sympy.solve((s * (s - a) * (s - b) * (s - c)) - (S**2), c)

    # tmpの回答分ループ処理
    for i in range(len(tmp)):
        # ゼロより大きい物だけを格納
        if tmp[i] > 0:
            ans.append(tmp[i])

    # 面積を戻り値として返す
    return ans

# メイン処理
if __name__ == '__main__':

    # 三角形ABCの辺 a = 7、b = 24、面積S =84
    a = 7
    b = 24
    S = 84

    print('辺c = ：', HeronToLine(a, b, S))

▼実行結果

辺c = ： [25]