■等速直線運動
速度が一定で物体が動き続ける運動を等速直線運動と言う。
すなわち、「平均の速さ」および「瞬間の速さ」も同じであるため、特段区別せず、速さを求めるだけで良い。
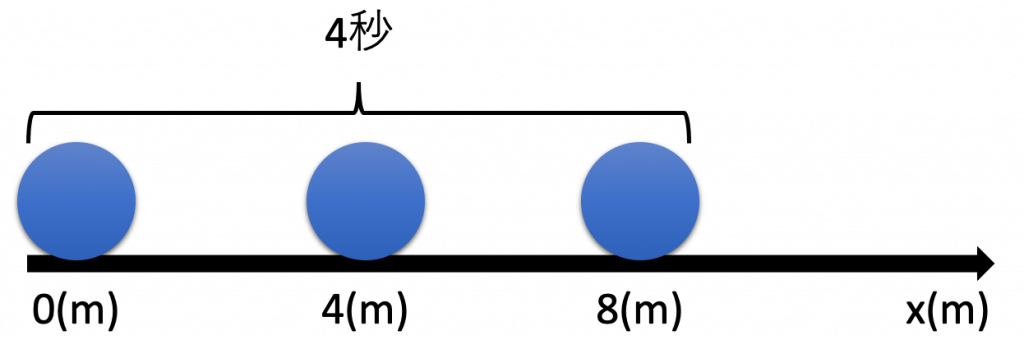
速さは、移動距離÷かかった時間で求めることができる。
例えば、8mの距離を4秒で移動した場合の速さは、2m/sである。
■例題
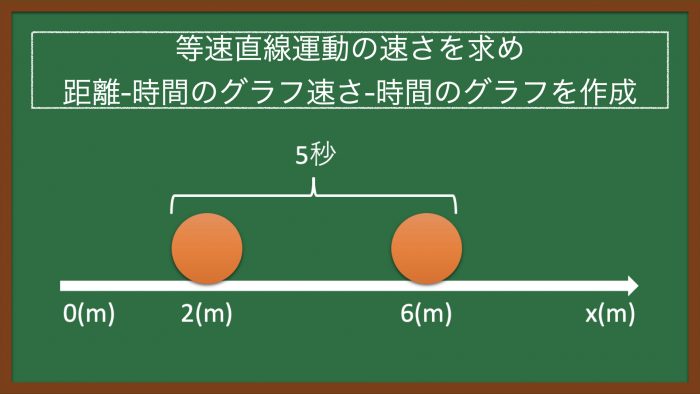
開始地点が2mであり、そこから5秒かけて6mまで進んだとき、以下の問題について、Pythonを使用して計算する。

(1)この物体の速さを求める。
(2)この物体の「時間-移動した距離」について、グラフを図示する。(0 ≦ 秒 ≦ 5)
(3)この物体の「時間-速さ」について、グラフを図示する。(0 ≦ 秒 ≦ 5)
▼(1)物体の速さ
等速直線運動の速さは「移動した距離」÷「時間」で求めることができる。
移動した距離:6 – 2 = 4m
移動した時間:5秒
したがって、求める速さは以下のソースを実行する。
・サンプルコード
# 速さを算出する処理
def cal_speed(time_s, distance):
return distance / time_s
# メイン処理
if __name__ == '__main__':
# 開始と終了距離をセット
start_distance = 2.0
end_distance = 6.0
# 時間をセット
time_s = 5.0
# 等速直線運動の速さを算出
speed = cal_speed(time_s ,end_distance - start_distance)
# 等速直線運動の速さを出力
print(speed, 'm/s')・実行結果
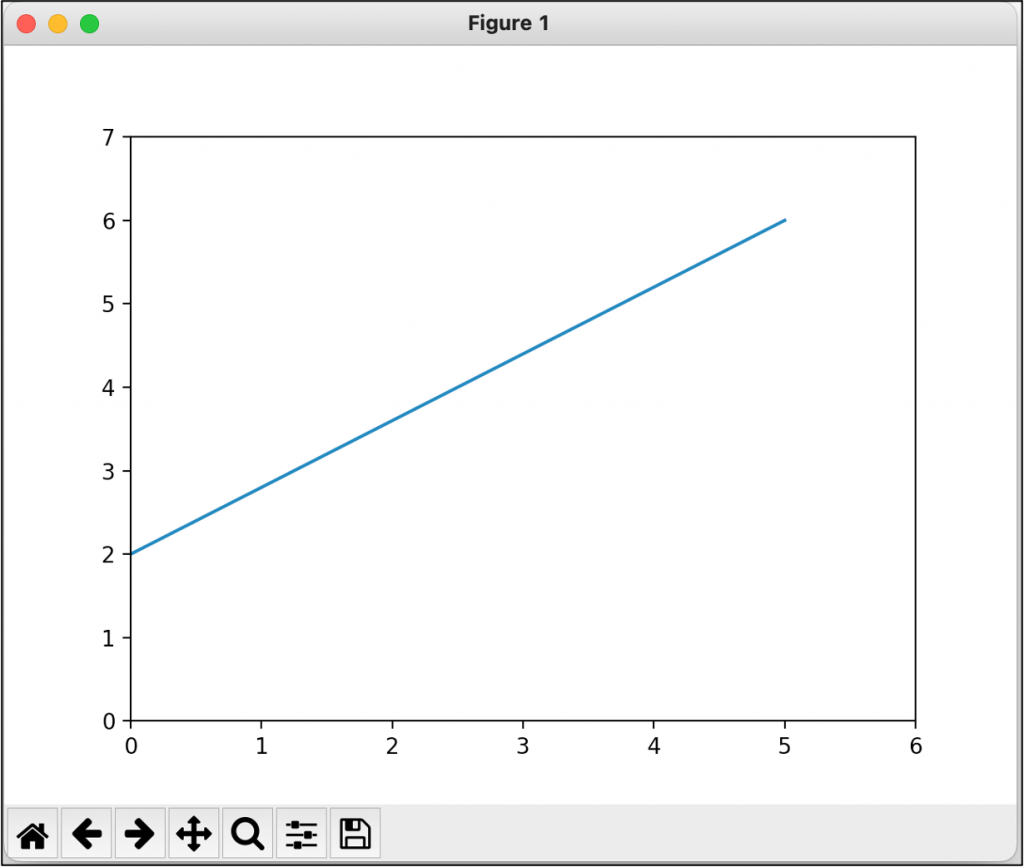
0.8 m/s▼(2)「時間-移動した距離」のグラフ
移動した距離とかかった時間に関するグラフを作成する。
インプットとして必要な情報は以下の通り。
・開始時点の距離(0秒の時の距離):2 m
・等速直線運動の速さ:0.8 m/s
・制約事項として、0秒から5秒までを図示する。
・サンプルコード
# 距離-時間のグラフを作成する関数
# 第1引数 :速度
# 第2引数 :開始距離
def MakeGraph_time_distance(speed, start_distance):
# 便宜上、0.1間隔で 0 <= t(s) < 5.1 の範囲を指定
t_min = 0
t_max = 5.1
t_interval = 0.1
t = np.arange(t_min, t_max, t_interval)
# x(m)を算出
x = speed * t + start_distance
# xの最大インデックスを取得
x_maxindex = np.argmax(x)
# xの最大値を取得
x_max = x[x_maxindex]
# x軸とy軸の範囲を設定
plt.xlim(0, 6)
plt.ylim(0, x_max + 1)
# グラフを作成
plt.plot(t,x)
# グラフを表示
plt.show()
# メイン処理
if __name__ == '__main__':
# 開始距離と速さをセット
start_distance = 2.0
speed = 0.8
# 時間-距離のグラフを表示
MakeGraph_time_distance(speed, start_distance)・実行結果
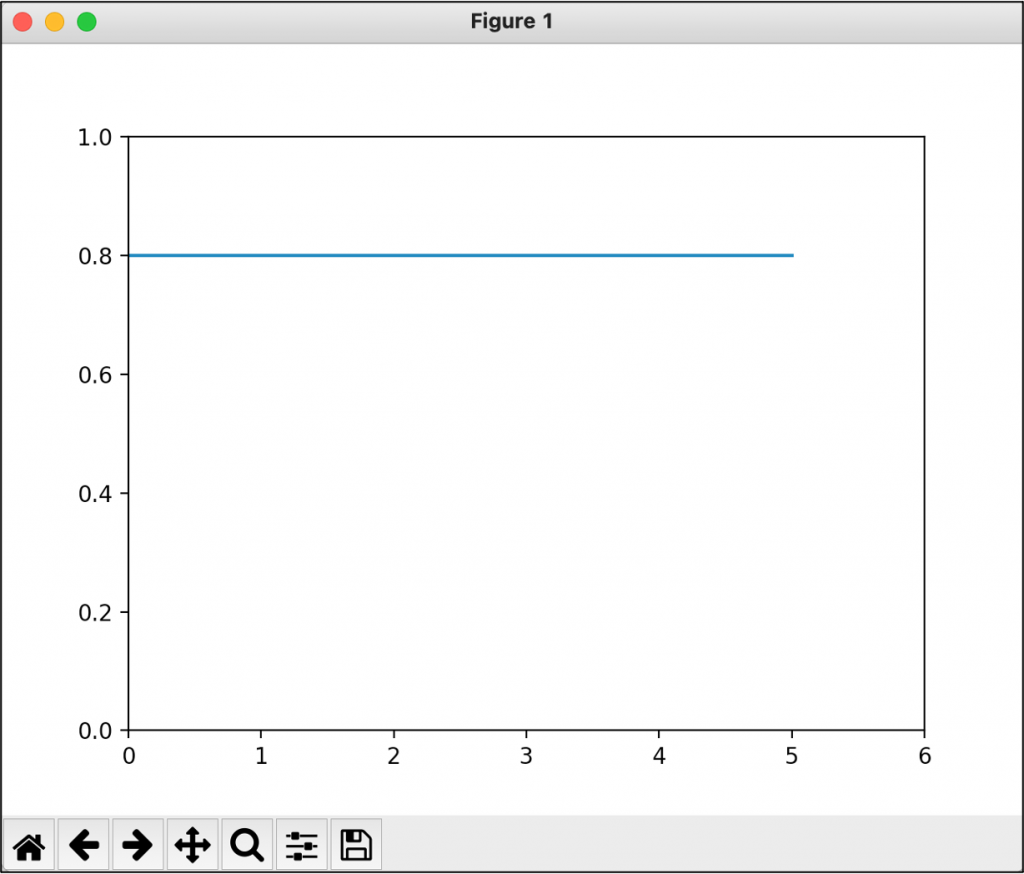
▼(3)「時間-移動した距離」のグラフ
移動した距離と速さに関するグラフを作成する。
インプットとして必要な情報は以下の通り。
・等速直線運動の速さ:0.8 m/s
・制約事項として、0秒から5秒までを図示する。
・サンプルコード
# 時間-速度のグラフを作成する関数
# 第1引数 :速度
def MakeGraph_time_speed(speed):
# 便宜上、0.1間隔で 0 <= t(s) < 5.1 の範囲を指定
t_min = 0
t_max = 5.1
t_interval = 0.1
t = np.arange(t_min, t_max, t_interval)
v = []
# v(m/s)を算出
for _ in range(len(t)):
v.append(speed)
# x軸とy軸の範囲を設定
plt.xlim(0, 6)
plt.ylim(0, 1)
# グラフを作成
plt.plot(t,v)
# グラフを表示
plt.show()
# メイン処理
if __name__ == '__main__':
# 等速直線運動の速さをセット
speed = 0.8
# 時間-速さのグラフを表示
MakeGraph_time_speed(speed)・実行結果


コメント